题目内容
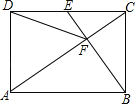
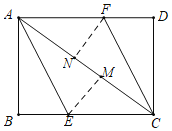
【题目】如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处.
(1)求证:四边形AECF是平行四边形;
(2)当∠BAE为多少度时,四边形AECF是菱形?请说明理由.
【答案】(1)证明见解析(2)当∠BAE=30°时,四边形AECF是菱形
【解析】
(1)首先证明△ABE≌△CDF,则DF=BE,然后可得到AF=EC,依据一组对边平行且相等四边形是平行四边形可证明AECF是平行四边形;
(2)由折叠性质得到∠BAE=∠CAE=30°,求得∠ACE=90°-30°=60°,即∠CAE=∠ACE,得到EA=EC,于是得到结论.
(1)∵四边形ABCD为矩形,
∴AB=CD,AD∥BC,∠B=∠D=90°,∠BAC=∠DCA.
由翻折的性质可知:∠EAB=![]() ∠BAC,∠DCF=
∠BAC,∠DCF=![]() ∠DCA.
∠DCA.
∴∠EAB=∠DCF.
在△ABE和△CDF中 ,
,
∴△ABE≌△CDF(ASA),
∴DF=BE.
∴AF=EC.
又∵AF∥EC,
∴四边形AECF是平行四边形;
(2)当∠BAE=30°时,四边形AECF是菱形,
理由:由折叠可知,∠BAE=∠CAE=30°,
∵∠B=90°,
∴∠ACE=90°-30°=60°,
即∠CAE=∠ACE,
∴EA=EC,
∵四边形AECF是平行四边形,
∴四边形AECF是菱形.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目