Question

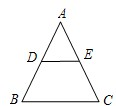如图，已知等腰△ABC的面积为8cm²，点D，E分别是AB，AC边的中点，则梯形DBCE的面积为

 

cm²．

Answer 1

分析：先利用DE是△ABC的中位线，可得DE∥BC，那么△ADE∽△ABC，就可得到两个三角形面积比等于相似比的平方，可求出S_△ADE，再根据S_梯形DSCE=S_△ABC-S_△ADE，可求出S_梯形DBCE．

解答：解：∵等腰△ABC的面积为8cm²，点D，E分别是AB，AC边的中点
∴DE=

1

2

BC，AD=

1

2

AB，AE=

1

2

AC
∴△ADE∽△ABC，相似比为

DE

BC

=

1

2

，面积比为

1

4

∴S_△ADE=

1

4

S_△ABC=

1

4

×8=2
故S_梯形DBCE=S_△ABC-S_△ADE=8-2=6cm²．

点评：本题考查的是三角形的中位线定理及相似三角形的性质，属较简单题目．