题目内容
20、梯形ABCD中，AD∥BC，AC⊥BD，若E，F，G，H分别是梯形ABCD各边AB、BC、CD、DA的中点．梯形ABCD满足
AB=CD
条件时，四边形EFGH是正方形．分析：要证明四边形EFGH是正方形，则要证明四边形EFGH的对角线垂直平分且相等．
解答：解：∵AD∥BC，AC⊥BD，且若E，F，G，H分别是梯形ABCD各边AB、BC、CD、DA的中点，
若四边形EFGH是正方形，
则梯形ABCD是等腰梯形，
故梯形ABCD满足AB=CD条件时，四边形EFGH是正方形．
若四边形EFGH是正方形，
则梯形ABCD是等腰梯形，
故梯形ABCD满足AB=CD条件时，四边形EFGH是正方形．
点评：本题是考查正方形的判别方法，判别一个四边形为正方形主要根据正方形的概念，途经有两种：
①先说明它是矩形，再说明有一组邻边相等；
②先说明它是菱形，再说明它有一个角为直角．
①先说明它是矩形，再说明有一组邻边相等；
②先说明它是菱形，再说明它有一个角为直角．
练习册系列答案
相关题目
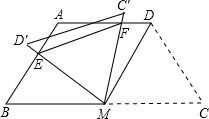如图，等腰梯形ABCD中，AD∥BC，AD=AB=CD=2，∠C=60°，M是BC的中点．
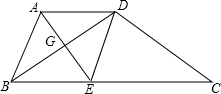DE．
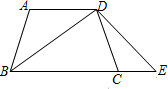如图，在梯形ABCD中，AD∥BC，AB=CD，点E在BC的延长线上，且∠BDE=∠ADC．求证：AB•BD=DE•AD．
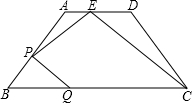如图，在等腰梯形ABCD中，AD∥BC，AB=5，AD=6，BC=12，点E在AD边上，且AE：ED=1：2，点P是AB边上的一个动点，（P不与A，B重合）过点P作PQ∥CE交BC于点Q，设AP=x，CQ=y，则y与x之间的函数关系是
分别交边CD、BC于点F、E，若AD=3，BC=12，