题目内容
已知:如图,在梯形ABCD中,AD∥BC,AB=AD,∠BAD的平分线AE分别交BD、BC于点G、E,连接 DE.
DE.(1)求证:四边形ABED是菱形;
(2)若ED⊥DC,∠ABC=60°,AB=2,求梯形ABCD的面积.
分析:(1)根据AB=AD及AE为∠BAD的平分线可得出BG=DG,从而证得△ADG≌△EGB,这样就得出四边形ABED为平行四边形,根据菱形的判定定理即可得出结论.
(2)过点D作DF⊥BC交BC于点F,根据四边形ABED是菱形,∠ABC=60°结合题意可得出BC的长度,进而利用解直角三角形的知识可得出DF的长度,也就得出了答案.
(2)过点D作DF⊥BC交BC于点F,根据四边形ABED是菱形,∠ABC=60°结合题意可得出BC的长度,进而利用解直角三角形的知识可得出DF的长度,也就得出了答案.
解答:解:(1)∵AB=AD,AE为∠BAD的平分线,
∴BG=DG,
∵AD∥BC,
∴∠ADG=∠GBE,∠DAG=∠GEB,
∴△ADG≌△EGB,
∴AG=GE,
∴四边形ABED为平行四边形,
∵AB=AD,
∴四边形ABED是菱形;
(2)过点D作DF⊥BC交BC于点F,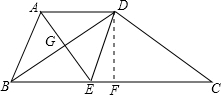
∵四边形ABED是菱形,∠ABC=60°,
∴∠DEC=∠ABC=60°,AD=BE=DE=AB=2.
∵ED⊥DC,
∴∠C=30°
∴EC=4,
∴BC=6,
在Rt△DEF中,∠DEF=60°,DE=2,
∴DF=
,(5分)
∴梯形ABCD的面积=
=4
.
∴BG=DG,
∵AD∥BC,
∴∠ADG=∠GBE,∠DAG=∠GEB,
∴△ADG≌△EGB,
∴AG=GE,
∴四边形ABED为平行四边形,
∵AB=AD,
∴四边形ABED是菱形;
(2)过点D作DF⊥BC交BC于点F,

∵四边形ABED是菱形,∠ABC=60°,
∴∠DEC=∠ABC=60°,AD=BE=DE=AB=2.
∵ED⊥DC,
∴∠C=30°
∴EC=4,
∴BC=6,
在Rt△DEF中,∠DEF=60°,DE=2,
∴DF=
| 3 |
∴梯形ABCD的面积=
(2+6)
| ||
| 2 |
| 3 |
点评:本题考查了梯形及菱形的判定以及菱形的性质,难度一般,解答本题的关键是熟练掌握菱形的判定定理及菱形的性质.

练习册系列答案
相关题目
 已知:如图,在梯形ABCD中,AD∥BC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,求AC的长及梯形面积S.
已知:如图,在梯形ABCD中,AD∥BC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,求AC的长及梯形面积S. 已知:如图,在梯形ABCD中,AD∥BC,∠B=45°,∠BAC=105°,AD=CD=4,
已知:如图,在梯形ABCD中,AD∥BC,∠B=45°,∠BAC=105°,AD=CD=4, 已知:如图,在梯形ABCD中,AB∥CD,AC⊥BC,AC平分∠DAB,点E为AC的中点.求证:DE=
已知:如图,在梯形ABCD中,AB∥CD,AC⊥BC,AC平分∠DAB,点E为AC的中点.求证:DE=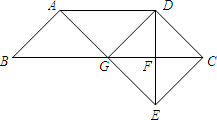 (2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G.
(2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G. 已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.
已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.