题目内容
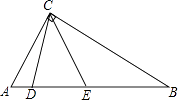
【题目】如图,直线AB、CD相交于点O,OM⊥AB,NO⊥CD,∠1= ![]() ∠BOC.
∠BOC.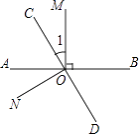
(1)求∠1的大小;
(2)求∠BON的大小.
【答案】
(1)解:∵OM⊥AB,
∴∠BOM=90°,
∵∠1= ![]() ∠BOC,
∠BOC,
∴∠1= ![]() ∠BOM=30°
∠BOM=30°
(2)解:∵OM⊥AB,
∴∠AOM=90°,
∵∠1=30°,
∴∠AOC=60°,
∴∠BOD=∠AOC=60°,
∵NO⊥CD,
∴∠DON=90°,
∴∠BON=∠BOD+∠DON=150°.
【解析】(1)根据两直线垂直得出∠BOM=90°,再由∠1=![]() ∠BOC,而∠1+∠∠BOM=∠BOC,因此可推出∠1=
∠BOC,而∠1+∠∠BOM=∠BOC,因此可推出∠1=![]() ∠BOM,计算即可求出结果。
∠BOM,计算即可求出结果。
(2)先根据已知OM⊥AB,NO⊥CD,得出∠DON的度数及∠AOC或∠BOD的度数,再根据∠BON=∠BOD+∠DON,代入计算即可求出结果。
【考点精析】掌握余角和补角的特征和对顶角和邻补角是解答本题的根本,需要知道互余、互补是指两个角的数量关系,与两个角的位置无关;两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目