题目内容
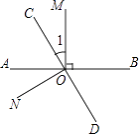
【题目】如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是( ) 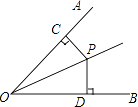
A.PC=PD
B.∠CPD=∠DOP
C.∠CPO=∠DPO
D.OC=OD
【答案】B
【解析】解:∵OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D, ∴PC=PD,故A正确;
在Rt△OCP与Rt△ODP中,![]() ,
,
∴△OCP≌△ODP,
∴∠CPO=∠DPO,OC=OD,故C、D正确.
不能得出∠CPD=∠DOP,故B错误.
故选B.
【考点精析】通过灵活运用角平分线的性质定理,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上即可以解答此题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目