题目内容
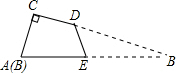 如图,有一张直角三角形纸片,两直角边AC=6cm,BC=9cm,将△ABC折叠,使点B与点A重合,折痕为DE,则CD等于( )cm.
如图,有一张直角三角形纸片,两直角边AC=6cm,BC=9cm,将△ABC折叠,使点B与点A重合,折痕为DE,则CD等于( )cm.A、
| ||
B、
| ||
C、
| ||
D、
|
分析:将△ABC折叠,使点B与点A重合,得到BD=AD,要求CD的长,设出未知数后,再表示出BD,再利用勾股定理求出x,从而得出答案.
解答:解:设CD长为xcm,则BD=(9-x)cm,
∵将△ABC折叠,使点B与点A重合,
∴AD=BD=(9-x)cm,
在Rt△ACD中,AC2+DC2=AD2,
∴62+x2=(9-x)2,
解得:x=
.
故选D.
∵将△ABC折叠,使点B与点A重合,
∴AD=BD=(9-x)cm,
在Rt△ACD中,AC2+DC2=AD2,
∴62+x2=(9-x)2,
解得:x=
| 5 |
| 2 |
故选D.
点评:此题主要考查了考查图形的翻折变换和勾股定理的综合运用,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,找准对应线段.

练习册系列答案
相关题目
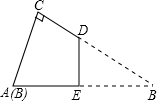 如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,点B与点A重合,折痕为DE,则CD的长为( )
如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,点B与点A重合,折痕为DE,则CD的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,有一张直角三角形纸片,两直角边AC=6 cm,BC=8cm,D是BC上一点,AD=DB,DE⊥AB,垂足为E,CD等于( )cm.
如图,有一张直角三角形纸片,两直角边AC=6 cm,BC=8cm,D是BC上一点,AD=DB,DE⊥AB,垂足为E,CD等于( )cm.A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,点B与点A重合,折痕为DE,则CD的长为
如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,点B与点A重合,折痕为DE,则CD的长为 如图,有一张直角三角形纸片,两直角边AC=6cm,BC=8cm,将△ABC折叠,使点B与点A重合,折痕为DE,求CD的长.
如图,有一张直角三角形纸片,两直角边AC=6cm,BC=8cm,将△ABC折叠,使点B与点A重合,折痕为DE,求CD的长.