题目内容
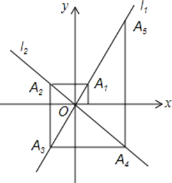
【题目】如图,一次函数![]() 的图像与x轴和y轴分别交于点A和B,再将
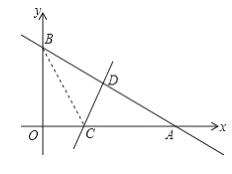
的图像与x轴和y轴分别交于点A和B,再将![]() 沿直线CD对折,使点A与点B重合,直线CD与x轴交于点C,与AB交于点D,连接BC.
沿直线CD对折,使点A与点B重合,直线CD与x轴交于点C,与AB交于点D,连接BC.
(1)求点A和点B的坐标;
(2)求![]() ;
;
(3)在y轴上有一点P,且![]() 是等腰三角形,求出点P的坐标.
是等腰三角形,求出点P的坐标.
【答案】(1)A的坐标为(4,0) B的坐标为(0,3)(2)![]() (3)(0,8)、(0,-2)、(0,-3)、(0,
(3)(0,8)、(0,-2)、(0,-3)、(0,![]() ).
).
【解析】
(1)令y=0求出x的值,再令x=0求出y的值,即可求出A、B两点的坐标.(2)根据勾股定理求出OC的长即可解决.(3)在y轴上有一点P,且△PAB是等腰三角形,分三种情况讨论,即当BP=BA时;当AP=AB时;当PB=PA时.
解:⑴因为A、B两点都在一次函数![]() 的直线上
的直线上
令y = 0则x = 4;令x = 0,则y = 3,
故点A的坐标为(4,0),点B的坐标为(0,3).
(2)设 OC =m,则 AC=CB =4-m
∵∠BOA = 90°,
∴![]() ,
,
![]() ,
,
解得![]() .
.
∴![]() ,
,
![]()
(3)∵A的坐标为(4,0),B的坐标为(0,3)
∴OB=3,OA=4,在Rt△OAB中
![]()
所以AB=5
当BP=BA时,P点可能在B点上方,也可能在B点下方,
当P点可能在B点上方时,OP=OB+BP=3+5=8,此时P点坐标为(0,8)
当P点可能在B点下方时,OP=BP-OB=5-3=2,此时P点坐标为(0,-2)
当AP=AB时,x轴为三角形ABP的垂直平分线,此时OB=OP,此时P点坐标为(0,-3)
当PB=PA时,设P点坐标为(0,n),![]()
整理得:6n+7=0,解得n=![]() ,故P点坐标为(0,
,故P点坐标为(0,![]() )
)
故点P的坐标为:0,8)、(0,-2)、(0,-3)、(0,![]() ).
).

【题目】在“朗读者”节目的影响下,某中学开展了“好书伴我成长”的读书活动,为了解3月份七年级300名学生读书情况,随机调查了七年级50个学生读书的册数,统计数据如下表所示:
册数 | 0 | 1 | 2 | 3 | 4 |
人数 | 4 | 12 | 16 | 17 | 1 |
关于这组数据,下列说法正确的是( )
A. 众数是 17 B. 平均数是 2 C. 中位数是 2 D. 方差是 2