Question

【题目】如图是某超市地下停车场入口的设计图，请根据图中数据计算CE的长度．（结果保留小数点后两位；参考数据：sin22°=0.3746，cos22°=0.9272，tan22°=0.4040）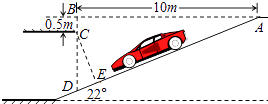

Answer 1

【答案】解：由已知有：∠BAE=22°，∠ABC=90°，∠CED=∠AEC=90° ∴∠BCE=158°，
∴∠DCE=22°，
又∵tan∠BAE= ，
∴BD=ABtan∠BAE，
又∵cos∠BAE=cos∠DCE= ，
∴CE=CDcos∠BAE
=（BD﹣BC）cos∠BAE
=（ ABtan∠BAE﹣BC）cos∠BAE
=（10×0.4040﹣0.5）×0.9272
≈3.28（m）．
【解析】通过解Rt△BAD求得BD=ABtan∠BAE，通过解Rt△CED求得CE=CDcos∠BAE．然后把相关角度所对应的函数值和相关的线段长度代入进行求值即可．