Question

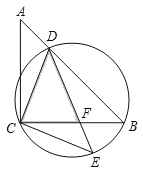
【题目】如图，以△ABC的一边AB为直径的半圆与其它两边AC，BC的交点分别为D、E，且点D为的中点．

（1）若∠A＝70°，求∠DBE的度数；

（2）求证：AB＝AC；

（3）若⊙O的半径为5cm，BC＝12cm，求线段BE的长．

Answer 1

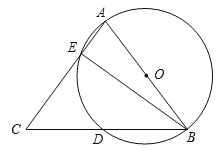
【答案】（1）35°；（2）详见解析；（3）．

【解析】

（1）点D为的中点，则OD⊥BE，且BH＝HE，∠ODB＝∠OBD＝（180°﹣70°）＝55°，∠OBE＝90°﹣70°＝20°，即可求解；

（2）由（1）得：OD是△ABC的中位线，则OD＝AC＝AB，即可求解；

（3）△ABC为等腰三角形，则cosC＝＝cos∠ODB，则sin∠ODB＝，BE＝2BH＝2BDsin∠ODB，即可求解．

（1）连接OD交BE于点H，连接AD，

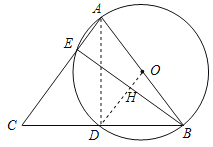
∵点D为的中点，则OD⊥BE，且BH＝HE，

AB为直径，则∠AEB＝90°，∴OD∥AC，且OD是△ABC的中位线，

∵∠CAB＝70°，则∠DOB＝70°，∠ODB＝∠OBD＝（180°﹣70°）＝55°

∠OBE＝90°﹣70°＝20°，

则∠DBE＝∠OBD﹣∠OBE＝55°﹣20°＝35°；

（2）由（1）得：OD是△ABC的中位线，则OD＝AC＝AB，

故AB＝AC；

（3）△ABC为等腰三角形，则cosC＝＝cos∠ODB，则sin∠ODB＝，

BE＝2BH＝2BDsin∠ODB＝2×6×＝．