题目内容
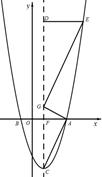
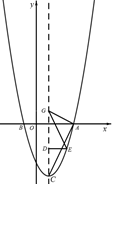
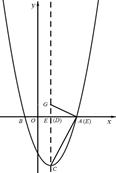
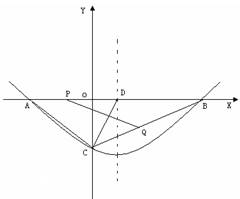
如图,已知二次函数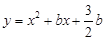 的图象与x轴交于A、B两点(B在A的左侧),顶点为C, 点D(1,m)在此二次函数图象的对称轴上,过点D作y轴的垂线,交对称轴右侧的抛物线于E点.
的图象与x轴交于A、B两点(B在A的左侧),顶点为C, 点D(1,m)在此二次函数图象的对称轴上,过点D作y轴的垂线,交对称轴右侧的抛物线于E点.

(1)求此二次函数的解析式和点C的坐标;
(2)当点D的坐标为(1,1)时,连接BD、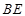 .求证:
.求证: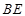 平分
平分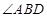 ;
;
(3)点G在抛物线的对称轴上且位于第一象限,若以A、C、G为顶点的三角形与以G、D、E为顶点的三角形相似,求点E的横坐标.
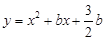 的图象与x轴交于A、B两点(B在A的左侧),顶点为C, 点D(1,m)在此二次函数图象的对称轴上,过点D作y轴的垂线,交对称轴右侧的抛物线于E点.
的图象与x轴交于A、B两点(B在A的左侧),顶点为C, 点D(1,m)在此二次函数图象的对称轴上,过点D作y轴的垂线,交对称轴右侧的抛物线于E点.
(1)求此二次函数的解析式和点C的坐标;
(2)当点D的坐标为(1,1)时,连接BD、
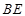 .求证:
.求证: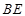 平分
平分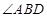 ;
;(3)点G在抛物线的对称轴上且位于第一象限,若以A、C、G为顶点的三角形与以G、D、E为顶点的三角形相似,求点E的横坐标.
(1)二次函数的解析式为 ;C(1,-4);
;C(1,-4);
(2)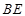 平分
平分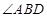 ;
;
(3)E点的横坐标为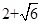 或
或 或
或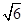 或
或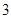 ..
..
 ;C(1,-4);
;C(1,-4);(2)
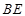 平分
平分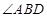 ;
;(3)E点的横坐标为
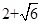 或
或 或
或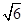 或
或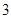 ..
..试题分析:解:(1)∵点D(1,m)在
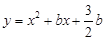 图象的对称轴上,
图象的对称轴上,∴
 .
.∴
 .
.∴二次函数的解析式为
 .
.∴C(1,-4).
(2)∵D(1,1),且DE垂直于y轴,
∴点E的纵坐标为1,DE平行于x轴.
∴
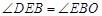 .
.令
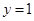 ,则
,则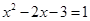 ,解得
,解得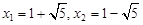 .
.∵点E位于对称轴右侧,
∴E
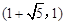 .
.∴D E =
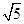 .
.令
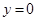 ,则
,则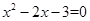 ,求得点A的坐标为(3,0),点B的坐标为(-1,0).
,求得点A的坐标为(3,0),点B的坐标为(-1,0).∴BD =
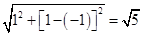 .
.∴BD =" D" E.
∴
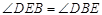 .
.∴
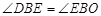 .
.∴
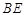 平分
平分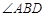 .
.(3)∵以A、C、G为顶点的三角形与以G、D、E为顶点的三角形相似,
且△GDE为直角三角形,
∴△ACG为直角三角形.
∵G在抛物线对称轴上且位于第一象限,
∴
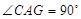 .
.∵A(3,0)C(1,-4),
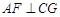 ,
,∴求得G点坐标为(1,1).
∴AG=
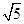 ,AC=
,AC=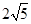 .
.∴AC="2" AG.
∴GD="2" DE或 DE ="2" GD.
设
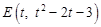 (t >1) ,
(t >1) , .当点D在点G的上方时,则DE="t" -1,
.当点D在点G的上方时,则DE="t" -1,GD = (
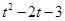 )
)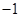 =
= .
.i.如图,当 GD="2" DE时,
则有,
 = 2(t-1).
= 2(t-1).解得,
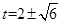 .(舍负)
.(舍负)ii. 如图3当DE =2GD时,

则有,t -1=2(
 ).
).解得,
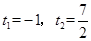 .(舍负)
.(舍负) . 当点D在点G的下方时,则DE="t" -1,
. 当点D在点G的下方时,则DE="t" -1,GD="1-" (
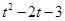 )= -
)= -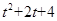 .
.i. 如图,当 GD="2" DE时,
则有,
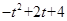 =2(t -1).
=2(t -1).解得,
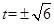 .(舍负)
.(舍负) ii. 如图,当DE ="2" GD时,
则有,t-1=2(
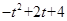 ).
).解得,
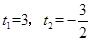 .(舍负)
.(舍负) 综上,E点的横坐标为
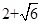 或
或 或
或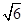 或
或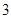 .
.
练习册系列答案
相关题目
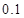 ,
,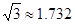 ).
).
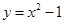 的图象上,则m的值为 ;平移此二次函数的图象,使点P与坐标原点重合,则平移后的函数图象所对应的解析式为 .
的图象上,则m的值为 ;平移此二次函数的图象,使点P与坐标原点重合,则平移后的函数图象所对应的解析式为 .




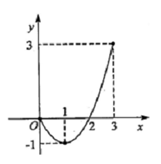
 向左平移2个单位,那么所得抛物线的表达式为
向左平移2个单位,那么所得抛物线的表达式为


