题目内容
【题目】如图,甲、乙两人分别从A(1, ![]() )、B(6,0)两点同时出发,点O为坐标原点,甲沿AO方向、乙沿BO方向均以4km/h的速度行驶,th后,甲到达M点,乙到达N点.
)、B(6,0)两点同时出发,点O为坐标原点,甲沿AO方向、乙沿BO方向均以4km/h的速度行驶,th后,甲到达M点,乙到达N点. 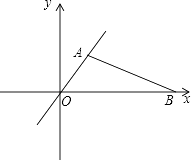
(1)请说明甲、乙两人到达O点前,MN与AB不可能平行;
(2)当t为何值时,△OMN∽△OBA;
(3)甲、乙两人之间的距离为MN的长,设s=MN2 , 求s与t之间的函数关系式,并求甲、乙两人之间距离的最小值.
【答案】
(1)证明:因为A坐标为(1, ![]() ),
),
所以OA=2,∠AOB=60°.
因为OM=2﹣4t,ON=6﹣4t,
当 ![]() =
= ![]() 时,解得t=0,
时,解得t=0,
即在甲、乙两人到达O点前,只有当t=0时,△OMN∽△OAB,所以MN与AB不可能平行
(2)证明:因为甲达到O点时间为t= ![]() ,乙达到O点的时间为t=
,乙达到O点的时间为t= ![]() =
= ![]() ,所以甲先到达O点,所以t=
,所以甲先到达O点,所以t= ![]() 或t=
或t= ![]() 时,O、M、N三点不能连接成三角形,
时,O、M、N三点不能连接成三角形,
①当t< ![]() 时,如果△OMN∽△OBA,则有
时,如果△OMN∽△OBA,则有 ![]() =
= ![]() ,解得t=2>
,解得t=2> ![]() ,所以,△OMN不可能相似△OBA;
,所以,△OMN不可能相似△OBA;
②当 ![]() <t<
<t< ![]() 时,∠MON>∠AOB,显然△OMN不相似△OBA;
时,∠MON>∠AOB,显然△OMN不相似△OBA;
③当t> ![]() 时,
时, ![]() =
= ![]() ,解得t=2>
,解得t=2> ![]() ,所以当t=2时,△OMN∽△OBA
,所以当t=2时,△OMN∽△OBA
(3)证明:①当t≤ ![]() 时,如图1,过点M作MH⊥x轴,垂足为H,
时,如图1,过点M作MH⊥x轴,垂足为H,
在Rt△MOH中,因为∠AOB=60°,
所以MH=OMsin60°=(2﹣4t)× ![]() =
= ![]() (1﹣2t),
(1﹣2t),
OH=0Mcos60°=(2﹣4t)× ![]() =1﹣2t,
=1﹣2t,
所以NH=(6﹣4t)﹣(1﹣2t)=5﹣2t,
所以s=[ ![]() (1﹣2t)]2+(5﹣2t)2=16t2﹣32t+28
(1﹣2t)]2+(5﹣2t)2=16t2﹣32t+28
②当 ![]() <t≤
<t≤ ![]() 时,如图2,作MH⊥x轴,垂足为H,
时,如图2,作MH⊥x轴,垂足为H,
在Rt△MOH中,MH= ![]() (4t﹣2)=
(4t﹣2)= ![]() (2t﹣1),NH=
(2t﹣1),NH= ![]() (4t﹣2)+(6﹣4t)=5﹣2t,
(4t﹣2)+(6﹣4t)=5﹣2t,
所以s=[ ![]() (1﹣2t)]2+(5﹣2t)2=16t2﹣32t+28
(1﹣2t)]2+(5﹣2t)2=16t2﹣32t+28
③当t> ![]() 时,同理可得s=[
时,同理可得s=[ ![]() (1﹣2t)]2+(5﹣2t)2=16t2﹣32t+28,
(1﹣2t)]2+(5﹣2t)2=16t2﹣32t+28,
综上所述,s=[ ![]() (1﹣2t)]2+(5﹣2t)2=16t2﹣32t+28.
(1﹣2t)]2+(5﹣2t)2=16t2﹣32t+28.
因为s=16t2﹣32t+28=16(t﹣1)2+12,
所以当t=1时,s有最小值为12,所以甲、乙两人距离最小值为2 ![]() km.
km.


【解析】(1)用反证法说明.根据已知条件分别表示相关线段的长度,根据三角形相似得比例式说明;(2)根据两个点到达O点的时间不同分段讨论解答;(3)在不同的时间段运用相似三角形的判定和性质分别求解析式,运用函数性质解答问题.
【考点精析】利用二次函数的最值和勾股定理的概念对题目进行判断即可得到答案,需要熟知如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案【题目】下框中是小明对一道题目的解答以及老师的批改.
题目:某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1,在温室内,沿前侧内墙保留3m的空地,其他三侧内墙各保留1m的通道,当温室的长与宽各为多少时,矩形蔬菜种植区域的面积是288m2? |
我的结果也正确!
(1)小明发现他解答的结果是正确的,但是老师却在他的解答中画了一条横线,并打了一个?.结果为何正确呢?
(2)请指出小明解答中存在的问题,并补充缺少的过程: 变化一下会怎样…
(3)如图,矩形A′B′C′D′在矩形ABCD的内部,AB∥A′B′,AD∥A′D′,且AD:AB=2:1,设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d,要使矩形A′B′C′D′∽矩形ABCD,a、b、c、d应满足什么条件?请说明理由. 

【题目】某校有学生2100人,在“文明我先行”活动中,开设了“法律、礼仪、环保、感恩、互助”五门校本课程,规定每位学生必须且只能选一门,为了解学生的报名意向,学校随机调查了100名学生,并制成统计表:校本课程意向统计表
课程类型 | 频数 | 频率(%) |
法律 | s | 0.08 |
礼仪 | a | 0.20 |
环保 | 27 | 0.27 |
感恩 | b | m |
互助 | 15 | 0.15 |
合计 | 100 | 1.00 |
请根据统计表的信息,解答下列问题;
(1)在这次调查活动中,学校采取的调查方式是(填写“普查”或“抽样调查”);
(2)a= , b= , m=;
(3)如果要画“校本课程报名意向扇形统计图”,那么“礼仪”类校本课程对应的扇形圆心角的度数是;
(4)请你估计,选择“感恩”类校本课程的学生约有人.


