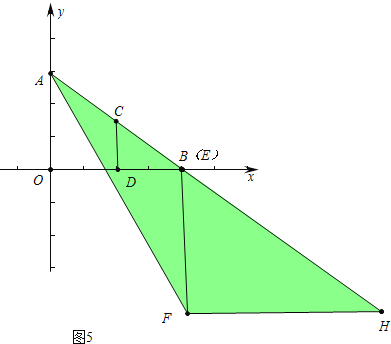
题目内容
【题目】如图,在直角坐标系中,点A(0,6),B(8,0),点C是线段AB的中点,CD⊥OB交OB于D,Rt△EFH的斜边EH在射线AB上,顶点F在射线AB的左侧,EF∥OA,点E从点A出发,以每秒1个单位的速度向B运动,到点B停止,AE=EF,运动时间为t(s).
(1)在Rt△EFH中,EF= ,EH= ,点F坐标为( , )(用含t的代数式表示)
(2)t为何值时,H与C重合?
(3)设△EFH与△CDB重叠部分图形的面积为S(S>0),求S与t的函数关系式。
(4)在整个运动过程中,Rt△EFH扫过的面积是多少?
【答案】(1)EF=t,EH=![]() 点F坐标为
点F坐标为![]() ;
;
(2)t=![]() 时,H与C重合;
时,H与C重合;
(3)当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]()
(4)Rt△EFH扫过的面积是![]() .
.
【解析】试题分析:(1)作EM⊥OA垂足为M,由△EFH∽△AOB,得![]() ,可以求出EH,由EM∥OB,得
,可以求出EH,由EM∥OB,得![]() ,可以解决点F坐标.
,可以解决点F坐标.
(2)根据AE+EH=AC,列出方程即可解决.
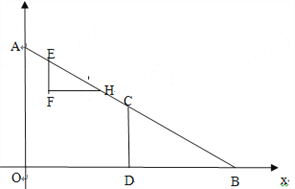
(3)分三种情形:①如图2中,FH与CD交于点M,当![]() 时,②如图3中,
时,②如图3中, ![]() <t≤5时,S=S△CDB=6,③如图4中,当5<t≤10时,画出图象求出重叠部分面积即可.
<t≤5时,S=S△CDB=6,③如图4中,当5<t≤10时,画出图象求出重叠部分面积即可.
(4)如图5中,在整个运动过程中Rt△EFH扫过的面积=S△AFH=![]() FH(AO+BF),由此即可计算.
FH(AO+BF),由此即可计算.
试题解析:(1)如图1中,作EM⊥OA垂足为M,
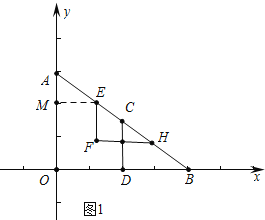
∵AE=EF=t,AO=6,BO=8,∠AOB=90°,
∴AB=![]() =10.
=10.
∵∠AOB=∠EFH=90°,∠EHF=∠ABO,
∴△EFH∽△AOB,
∴![]() ,即
,即![]() ,
,
∴EH=![]() t,
t,
∵EM∥OB,
∴![]() ,
,
∴AM=![]() t,EMspan>=
t,EMspan>=![]() t,
t,
∴点F坐标(![]() t,6-
t,6-![]() t).
t).
(2)如图2中,当点H与点C重合时,
AE+EH=AC,
∴t+![]() t=5,
t=5,
∴t=![]()
∴t=![]() 时,点H与点C重合.
时,点H与点C重合.
(3)当点H与点B重合时,AE+EH=AB,
∴t+![]() t=10,
t=10,
∴t=![]() ,
,
当点E与点C重合时,t=5,
当点E与点B重合时,t=10,
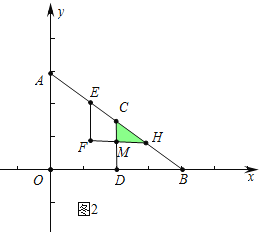
①如图2中,FH与CD交于点M,当![]() ≤t≤
≤t≤![]() 时,
时,
∵CH=EH-EC=EH-(AC-AE)=![]() t-5+t=
t-5+t=![]() t-5.CM=
t-5.CM=![]() CH=
CH=![]() t-3,MH=
t-3,MH=![]() CH=
CH=![]() t-4,
t-4,
∴S=![]() CMMH=
CMMH=![]() (
(![]() t-3)(
t-3)(![]() t-4)=
t-4)=![]() t2-
t2-![]() t+6.
t+6.
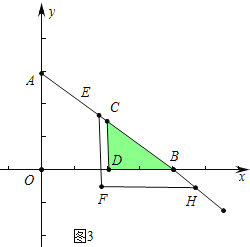
②如图3中, ![]() <t≤5时,S=S△CDB=6,
<t≤5时,S=S△CDB=6,
③如图4中,当5<t≤10时,
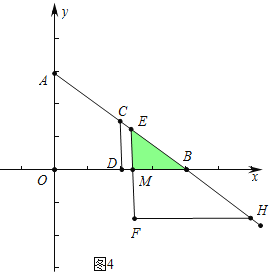
∵EB=AB-AE=10-t,EM=![]() EB=6-
EB=6-![]() t,BM=
t,BM=![]() EB=8-
EB=8-![]() t,
t,
∴S=![]() EMMB=
EMMB=![]() (6-
(6-![]() t)(8-
t)(8-![]() t)=
t)=![]() (10-t)2.
(10-t)2.
综上所述: ![]() ,
, ![]() ,
, ![]()
(4)如图5中,在整个运动过程中Rt△EFH扫过的面积=S△AFH=![]() FH(AO+BF)=
FH(AO+BF)=![]() ×
×![]() ×16=
×16=![]() .
.