题目内容
【题目】一次函数y=ax+b(a≠0)、二次函数y=ax2+bx和反比例函数y= ![]() (k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(﹣2,0),则下列结论中,正确的是( )
(k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(﹣2,0),则下列结论中,正确的是( ) 
A.b=2a+k
B.a=b+k
C.a>b>0
D.a>k>0
【答案】D
【解析】解:∵根据图示知,一次函数与二次函数的交点A的坐标为(﹣2,0), ∴﹣2a+b=0,
∴b=2a.
∵由图示知,抛物线开口向上,则a>0,
∴b>0.
∵反比例函数图象经过第一、三象限,
∴k>0.
A、由图示知,双曲线位于第一、三象限,则k>0,
∴2a+k>2a,即b<2a+k.
故A选项错误;
B、∵k>0,b=2a,
∴b+k>b,
即b+k>2a,
∴a=b+k不成立.
故B选项错误;
C、∵a>0,b=2a,
∴b>a>0.
故C选项错误;
D、观察二次函数y=ax2+bx和反比例函数y= ![]() (k≠0)图象知,当x=﹣
(k≠0)图象知,当x=﹣ ![]() =﹣
=﹣ ![]() =﹣1时,y=﹣k>﹣
=﹣1时,y=﹣k>﹣ ![]() =﹣
=﹣ ![]() =﹣a,即k<a,
=﹣a,即k<a,
∵a>0,k>0,
∴a>k>0.
故D选项正确;
故选:D.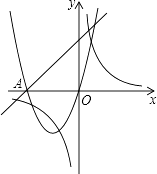
【考点精析】根据题目的已知条件,利用一次函数的图象和性质和反比例函数的图象的相关知识可以得到问题的答案,需要掌握一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远;反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点.

【题目】为了增强公民的节水意识,合理利用水资源,某市采用价格调控手段来引导市民节约用水:每户居民每月用水不超过15立方米时,按基本价格x元/立方米进行收费;超过15立方米时,加价收费,超过的部分按y元/立方米收费.该市某户居民今年3、4、5月份的用水量和水费如下表所示:
月份 | 用水量(立方米) | 水费(元) |
3 | 16 | 50 |
4 | 20 | 70 |
5 | m | 不低于36元且不超过95元 |
(1)求x、y的值;
(2)求该居民5月份用水量m的范围.
【题目】某校为了做好大课间活动,计划用400元购买10件体育用品,备选体育用品及单价如下表(单位:元)
备选体育用品 | 篮球 | 排球 | 羽毛球拍 |
单价(元) | 50 | 40 | 25 |
(1)若400元全部用来购买篮球和羽毛球拍共10件,问篮球和羽毛球拍各购买多少件?
(2)若400元全部用来购买篮球、排球和羽毛球拍三种共10件,能实现吗?(若能实现直接写出一种答案即可,若不能请说明理由.)