Question

如图已知AB是⊙O的直径，BC是弦，弦BD平分∠ABC交AC于F，弦DE⊥AB于H，交AC于G．
①求证：AG=GD；
②当∠ABC满足什么条件时，△DFG是等边三角形？
③若AB=10，sin∠ABD=

3

5

，求BC的长．

Answer 1

分析：（1）首先连接AD，由DE⊥AB，AB是⊙O的直径，根据垂径定理，即可得

AD

=

AE

，然后根据在同圆或等圆中，同弧或等弧所对的圆周角相等，证得∠ADE=∠ABD，又由弦BD平分∠ABC，易证得∠ADE=∠DAC，根据等角对等边的性质，即可证得AG=GD；
（2）当∠ABC=60°时，△DFG是等边三角形，根据半圆（或直径）所对的圆周角是直角与三角形外角的性质，易求得∠DGF=∠DFG=60°，即可证得结论；
（3）利用三角函数的性质，等角的三角函数值相等，即可求得答案．

解答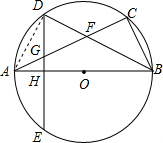：（1）证明：连接AD，
∵DE⊥AB，AB是⊙O的直径，
∴

AD

=

AE

，
∴∠ADE=∠ABD，
∵弦BD平分∠ABC，
∴∠DBC=∠ABD，
∵∠DBC=∠DAC，
∴∠ADE=∠DAC，
∴AG=GD；

（2）解：当∠ABC=60°时，△DFG是等边三角形．
理由：∵弦BD平分∠ABC，
∴∠DBC=∠ABD=30°，
∵AB是⊙O的直径，
∴∠ACB=90°，
∴∠CAB=90°-∠ABC=30°，
∴∠DFG=∠FAB+∠DBA=60°，
∵DE⊥AB，
∴∠DGF=∠AGH=90°-∠CAB=60°，
∴△DGF是等边三角形；

（3）解：∵AB是⊙O的直径，
∴∠ADB=∠ACB=90°，
∵∠DAC=∠DBC=∠ABD，
∵AB=10，sin∠ABD=

3

5

，
∴在Rt△ABD中，AC=AB•sin∠ABD=6，
∴AD=

AB2-AD2

=8，
∴tan∠ABD=

AD

BD

=

3

4

，cos∠ABD=

BD

AB

=

4

5

，
在Rt△ADF中，DF=AD•tan∠DAF=AD•tan∠ABD=6×

3

4

=

9

2

，
∴BF=BD-DF=8-

9

2

=

7

2

，
∴在Rt△BCF中，BC=BF•cos∠DBC=BF•cos∠ABD=

7

2

×

4

5

=

14

5

．
∴BC的长为：

14

5

．

点评：此题考查了圆周角定理、垂径定理、直角三角形的性质、三角函数的性质以及勾股定理等知识．此题综合性较强，难度较大，解题的关键是掌握数形结合思想与转化思想的应用，注意辅助线的作法．