Question

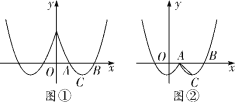
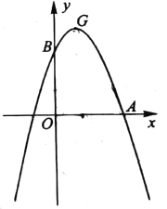
【题目】如图，抛物线与轴正半轴，轴正半轴分别交于点，且点为抛物线的顶点．

求抛物线的解析式及点G的坐标；

点为抛物线上两点(点在点的左侧) ，且到对称轴的距离分别为个单位长度和个单位长度，点为抛物线上点之间(含点)的一个动点，求点的纵坐标的取值范围．

Answer 1

【答案】（1），G（1,4）；（2）﹣21≤≤4.

【解析】

（1）根据用c表示出点A的坐标，把A的坐标代入函数解析式，得到一个关于c的一元二次方程，解出c的值，从而求出函数解析式，求出顶点G的坐标．

（2）根据函数解析式求出函数图像对称轴，根据点M,N到对称轴的距离，判断出M,N的横坐标，进一步得出M,N的纵坐标，求出M,N点的坐标后可确定的取值范围．

解：（1）∵抛物线与轴正半轴分别交于点B，

∴B点坐标为（c，0），

∵抛物线经过点A，

∴﹣c2+2c+c=0，

解得c1=0（舍去），c2=3，

∴抛物线的解析式为

∵=﹣（x－1）2+4，

∴抛物线顶点G坐标为（1,4）．

（2）抛物线的对称轴为直线x=1，

∵点M,N到对称轴的距离分别为3个单位长度和5个单位长度 ，

∴点M的横坐标为﹣2或4，点N的横坐标为﹣4或6，

点M的纵坐标为﹣5，点N的纵坐标为﹣21，

又∵点M在点N的左侧，

∴当M坐标为（﹣2，﹣5）时，点N的坐标为（6，﹣21），

则﹣21≤≤4

当当M坐标为（4，﹣5）时，点N的坐标为（6，﹣21），

则﹣21≤≤﹣5，

∴的取值范围为﹣21≤≤4．