ЬтФПФкШн
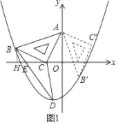
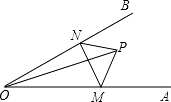
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌНЋвЛПщбќГЄЮЊ5ЕФЕШбќжБНЧШ§НЧАхABCЗХдкЕкЖўЯѓЯоЃЌЧваБППдкСНзјБъжсЩЯЃЌжБНЧЖЅЕуCЕФзјБъЮЊЃЈЉ1ЃЌ0ЃЉЃЌЕуBдкХзЮяЯпy=ax2+axЉ2ЩЯЃЎ
ЃЈ1ЃЉЕуAЕФзјБъЮЊ ЃЌЕуBЕФзјБъЮЊ ЃЛ
ЃЈ2ЃЉХзЮяЯпЕФЙиЯЕЪНЮЊ ЃЛ
ЃЈ3ЃЉЩшЃЈ2ЃЉжаХзЮяЯпЕФЖЅЕуЮЊDЃЌЧѓЁїDBCЕФУцЛ§ЃЛ
ЃЈ4ЃЉНЋШ§НЧАхABCШЦЖЅЕуAФцЪБеыЗНЯђа§зЊ90ЁуЃЌЕНДяЁїABЁфCЕФЮЛжУЃЎЧыХаЖЯЕуBЁфCЁфЪЧЗёдкЃЈ2ЃЉжаЕФХзЮяЯпЩЯЃЌВЂЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉЃЈ0ЃЌ2ЃЉЃЌЃЈЉ3ЃЌ1ЃЉЃЛ
ЃЈ2ЃЉy=0.5x2+0.5xЉ2ЃЛ
ЃЈ3ЃЉSЁїBCD=![]() ЃЛ
ЃЛ
ЃЈ4ЃЉЕуBЁфЁЂCЁфдкЃЈ2ЃЉжаЕФХзЮяЯпЩЯЃЎРэгЩМћНтЮі.
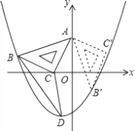
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉЧѓAЕуЕФзјБъОЭЪЧЧѓOAЕФГЄЃЌПЩдкжБНЧШ§НЧаЮOACжаЃЌИљОнAC=5ЃЌOC=1РДЧѓГіOAЕФГЄЃЌМДПЩЕУГіAЕФзјБъЃЎШчЙћЙ§BзїxжсЕФДЙЯпЃЌМйЩшДЙзуЮЊFЃЌФЧУДЁїACOЁеЁїCBHЃЌOA=CFЃЌBF=OCЃЌгЩДЫПЩЧѓГіBЕФзјБъЃЛ
ЃЈ2ЃЉНЋвбОЧѓГіЕФAЃЌBЕФзјБъДњШыХзЮяЯпЕФНтЮіЪНжаМДПЩЧѓГіХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ3ЃЉИљОнЃЈ2ЃЉЕФКЏЪ§ЙиЯЕЪНМДПЩЧѓГіDЕуЕФзјБъЃЎЧѓЁїDBCЕФУцЛ§ЪБЃЌПЩНЋЁїDBCЗжГЩЁїCBEКЭЁїDCEСНВПЗжЃЈМйЩшBDНЛxжсгкEЃЉЃЎПЩЯШИљОнBЃЌDЕФзјБъЧѓГіBDЫљдкжБЯпЕФНтЮіЪНЃЌНјЖјЧѓГіEЕуЕФзјБъЃЌФЧУДПЩЧѓГіCEЕФГЄЃЌШЛКѓвдBЃЌDСНЕуЕФзнзјБъЕФОјЖджЕЗжБ№зїЮЊЁїBCEКЭЁїDCEЕФИпЃЌМДПЩЧѓГіЁїDBCЕФУцЛ§ЃЛЃЈ4ЃЉБОЬтЕФЙиМќЪЧЧѓГіBЁфЃЌCЁфСНЕуЕФзјБъЃЎЙ§ЕуBЁфзїBЁфMЁЭyжсгкЕуMЃЌЙ§ЕуBзїBNЁЭyжсгкЕуNЃЌЙ§ЕуCЁхзїCЁхPЁЭyжсгкЕуPЃЎШЛКѓЗТееЃЈ1ЃЉжаЧѓзјБъЪБЕФЗНЗЈЃЌЭЈЙ§жЄRtЁїABЁфMЁеRtЁїBANРДЕУГіBЁфЕФзјБъЃЎЭЌРэПЩЕУГіCЁфЕФзјБъЃЎШЛКѓНЋСНЕуЕФзјБъЗжБ№ДњШыХзЮяЯпЕФНтЮіЪНжаЃЌНјЖјПЩХаЖЯГіСНЕуЪЧЗёдкХзЮяЯпЩЯЃЎ
БОЬтНтЮіЃКЃЈ1ЃЉЁпCЃЈ1ЃЌ0ЃЉЃЌЁрOC=1ЃЌЁпAC=![]() ЃЌЁрOA=
ЃЌЁрOA=![]() =2ЃЌЁрAЃЈ0ЃЌ2ЃЉЃЌ
=2ЃЌЁрAЃЈ0ЃЌ2ЃЉЃЌ
зїBHЁЭxжсгкHЃЌШчЭМ1ЃЌЁпЁїACBЮЊЕШбќжБНЧШ§НЧаЮЃЌЁрCA=CBЃЌЁЯACB=90ЁуЃЌ
ЁпЁЯACO+ЁЯBCH=90ЁуЃЌЁЯACO+ЁЯCAO=90ЁуЃЌЁрЁЯCAO=ЁЯBCHЃЌ
дкЁїACOКЭЁїCBHжа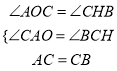 ЃЌЁрЁїACOЁеЁїCBHЃЌЁрOC=BH=1ЃЌAO=CH=2ЃЌЁрBЃЈЉ3ЃЌ1ЃЉЃЛ
ЃЌЁрЁїACOЁеЁїCBHЃЌЁрOC=BH=1ЃЌAO=CH=2ЃЌЁрBЃЈЉ3ЃЌ1ЃЉЃЛ
ЙЪД№АИЮЊЃЈ0ЃЌ2ЃЉЃЌЃЈЉ3ЃЌ1ЃЉЃЛ
ЃЈ2ЃЉАбBЃЈЉ3ЃЌ1ЃЉДњШыy=ax2+axЉ2ЕУ9aЉ3aЉ2=1ЃЌНтЕУa=0.5ЃЌЁрХзЮяЯпНтЮіЪНЮЊy=0.5x2+0.5xЉ2ЃЛ
ЙЪД№АИЮЊy=0.5x2+0.5xЉ2ЃЛ
ЃЈ3ЃЉЁпy=0.5x2+0.5xЉ2=0.5ЃЈx+0.5ЃЉ2Љ![]() ЃЌЁрDЃЈЉ0.5ЃЌЉ
ЃЌЁрDЃЈЉ0.5ЃЌЉ![]() ЃЉЃЌЩшжБЯпBDЕФЙиЯЕЪНЮЊy=kx+bЃЌ
ЃЉЃЌЩшжБЯпBDЕФЙиЯЕЪНЮЊy=kx+bЃЌ
НЋBЃЈЉ3ЃЌ1ЃЉЁЂDЃЈЉ0.5ЃЌЉ![]() ЃЉДњШыЕУ
ЃЉДњШыЕУ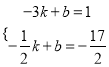 ЃЌНтЕУ
ЃЌНтЕУ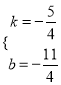 ЃЌ
ЃЌ
ЁрBDЕФЙиЯЕЪНЮЊy=Љ![]() xЉ
xЉ![]() ЃЛжБЯпBDКЭxжсНЛЕуЮЊEЃЌШчЭМ1ЃЌ
ЃЛжБЯпBDКЭxжсНЛЕуЮЊEЃЌШчЭМ1ЃЌ
ЕБy=0ЪБЃЌЉ![]() xЉ
xЉ![]() =0ЃЌНтЕУx=Љ2.2ЃЌдђEЃЈЉ2.2ЃЌ0ЃЉЃЌ
=0ЃЌНтЕУx=Љ2.2ЃЌдђEЃЈЉ2.2ЃЌ0ЃЉЃЌ
ЁрSЁїBCD=SЁїBCE+SЁїDCE=0.5ЁЄЃЈЉ1+2.2ЃЉЁЄ1+0.5ЁЄЃЈЉ1+2.2ЃЉЁЄ![]() =
=![]() ЃЛ
ЃЛ
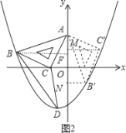
ЃЈ4ЃЉЕуBЁфЁЂCЁфдкЃЈ2ЃЉжаЕФХзЮяЯпЩЯЃЎРэгЩШчЯТЃК
ШчЭМ2ЃЌЙ§ЕуBЁфзїBЁфNЁЭyжсгкЕуNЃЌЙ§ЕуBзїBFЁЭyжсгкЕуFЃЌЙ§ЕуCЁфзїCЁфMЁЭyжсгкЕуMЃЌ
ЁпШ§НЧАхABCШЦЖЅЕуAФцЪБеыЗНЯђа§зЊ90ЁуЃЌЕНДяЁїABЁфCЕФЮЛжУЃЌ
ЁрЁЯCACЁф=90ЁуЃЌЁЯBABЁф=90ЁуЃЌAC=ACЁфЃЌAB=ABЁфЃЌ
ЁпЁЯBAF+ЁЯBЁфAN=90ЁуЃЌЁЯBAF+ЁЯABF=90ЁуЃЌЁрЁЯABF=ЁЯBЁфANЃЌ
дкRtЁїABЁфNгыRtЁїBAFжаЃЌ 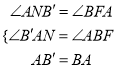 ЃЌЁрRtЁїABЁфNЁеRtЁїBAFЃЌ
ЃЌЁрRtЁїABЁфNЁеRtЁїBAFЃЌ
ЁрBЁфN=AF=2ЃЌAN=BF=3ЃЌЁрBЁфЃЈ1ЃЌЉ1ЃЉЃЌЭЌРэПЩЕУЁїACЁфMЁеЁїCAOЃЌ
ЁрCЁфM=OA=2ЃЌAM=OC=1ЃЌЁрCЁфЃЈ2ЃЌ1ЃЉЃЌ
ЕБx=1ЪБЃЌy=![]() x2+
x2+![]() xЉ2=
xЉ2=![]() +
+![]() Љ2=Љ1ЃЌЫљвдЕуBЁфЃЈ1ЃЌЉ1ЃЉдкХзЮяЯпЩЯЃЌ
Љ2=Љ1ЃЌЫљвдЕуBЁфЃЈ1ЃЌЉ1ЃЉдкХзЮяЯпЩЯЃЌ
ЕБx=2ЪБЃЌy=![]() x2+
x2+![]() xЉ2=2+1Љ2=1ЃЌЫљвдЕуCЁфЃЈ2ЃЌ1ЃЉдкХзЮяЯпЩЯЃЎ
xЉ2=2+1Љ2=1ЃЌЫљвдЕуCЁфЃЈ2ЃЌ1ЃЉдкХзЮяЯпЩЯЃЎ