题目内容
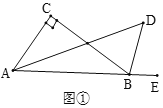
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 匀速运动,同时点
匀速运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点
匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点![]() 运动的时间是
运动的时间是![]() 秒(
秒(![]() ).过点
).过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() .
.

(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)四边形![]() 能够成为菱形吗?如果能,求出相应的
能够成为菱形吗?如果能,求出相应的![]() 值;如果不能,请说明理由;
值;如果不能,请说明理由;
(3)当![]() 为何值时,
为何值时,![]() 为直角三角形?请说明理由.
为直角三角形?请说明理由.
【答案】(1)证明见详解(2)当![]() 时,四边形
时,四边形![]() 能够成为菱形;理由见详解(3)当
能够成为菱形;理由见详解(3)当![]() 或
或![]() 时,
时,![]() 为直角三角形;理由见详解
为直角三角形;理由见详解
【解析】
(1)根据时间和速度表示出![]() ,
,![]() ,再利用
,再利用![]() 角所对的直角边等于斜边的一半求得
角所对的直角边等于斜边的一半求得![]() ,则可得
,则可得![]() ,然后根据平行线的判定得到
,然后根据平行线的判定得到![]() ,即可得证结论;
,即可得证结论;
(2)由(1)的结论可得四边形![]() 是平行四边形,若
是平行四边形,若![]() 为菱形,则必有邻边相等,则
为菱形,则必有邻边相等,则![]() ,列出关于
,列出关于![]() 的方程求解即可;
的方程求解即可;
(3)当![]() 为直角三角形时,分三种情况分别找等量关系列方程求解即可.
为直角三角形时,分三种情况分别找等量关系列方程求解即可.
解:(1)根据题意得:![]() ,
,![]()
∵![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴四边形![]() 是平行四边形;
是平行四边形;
(2)结论:四边形![]() 能够成为菱形
能够成为菱形
理由:由(1)可知四边形![]() 是平行四边形
是平行四边形
若![]() 为菱形,则
为菱形,则![]() ,如图:
,如图:
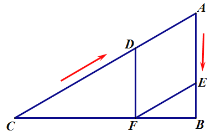
∵![]() ,
,![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴当![]() 时,四边形
时,四边形![]() 能够成为菱形;
能够成为菱形;
(3)①当![]() 时,如图:
时,如图:
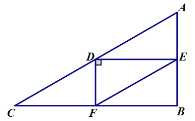
∵![]() ,
,![]()
∴四边形![]() 为矩形
为矩形
∴![]()
∵由(1)可知四边形![]() 是平行四边形
是平行四边形
∴![]()
∵由(1)可知![]() ,
,![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∴![]() ;
;
②当![]() 时,如图:
时,如图:
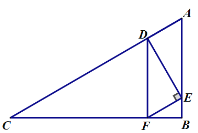
∵由(1)可知四边形![]() 是平行四边形
是平行四边形
∴![]()
∴![]()
∵在![]() 中,
中,![]()
∴![]()
∵![]()
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]()
∴![]() ;
;
③当![]() 时,不成立;
时,不成立;
∴综上所述,当![]() 或
或![]() 时,
时,![]() 为直角三角形.
为直角三角形.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目