题目内容
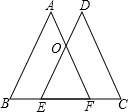 如图,已知点E、F在BC上,AF、DE相交于O点,且BE=CF,AB=CD,∠B=∠C,那么AO=DO吗?说明你的理由.
如图,已知点E、F在BC上,AF、DE相交于O点,且BE=CF,AB=CD,∠B=∠C,那么AO=DO吗?说明你的理由.分析:求出BF=CE,根据SAS证△ABF≌△DCE,推出AF=DE,∠AFB=∠DEC,推出OE=OF即可.
解答:解:OA=OD,
理由是:∵BE=CF,
∴BE+EF=CF+EF,
∴BF=CE,
∵在△ABF和△DCE中
,
∴△ABF≌△DCE(SAS),
∴AF=DE,∠AFB=∠DEC,
∴OE=OF,
∴AF-OF=DE-OE,
∴OA=OD.
理由是:∵BE=CF,
∴BE+EF=CF+EF,
∴BF=CE,
∵在△ABF和△DCE中
|
∴△ABF≌△DCE(SAS),
∴AF=DE,∠AFB=∠DEC,
∴OE=OF,
∴AF-OF=DE-OE,
∴OA=OD.
点评:本题考查了全等三角形的性质和判定,等腰三角形的性质和判定,关键是根据全等三角形性质和等腰三角形的性质得出AF=DE和OE=OF.

练习册系列答案
相关题目
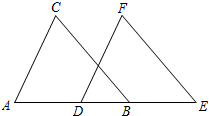 如图,已知点B、D在直线AE上,AC∥DF,∠C=∠F,AD=BE,试说明BC∥EF的理由.
如图,已知点B、D在直线AE上,AC∥DF,∠C=∠F,AD=BE,试说明BC∥EF的理由. BD于点E,BD=8,CM=2.
BD于点E,BD=8,CM=2. (2013•建邺区一模)如图,已知点E,C在线段BF上,BE=EC=CF,AB∥DE,∠ACB=∠F.
(2013•建邺区一模)如图,已知点E,C在线段BF上,BE=EC=CF,AB∥DE,∠ACB=∠F. 如图,已知点A,B分别在x轴和y轴上,且OA=OB=
如图,已知点A,B分别在x轴和y轴上,且OA=OB= 如图,已知点D、F在线段BC上,点E在线段BA的延长线上,EF与AC交于点G,且∠EFC=∠ADC,∠AGE=∠E.请说出AD平分∠BAC的理由.
如图,已知点D、F在线段BC上,点E在线段BA的延长线上,EF与AC交于点G,且∠EFC=∠ADC,∠AGE=∠E.请说出AD平分∠BAC的理由.