题目内容
如图,已知点C、D在以O为圆心,AB为直径的半圆上,且OC⊥BD于点M,CF⊥AB于点F交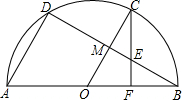 BD于点E,BD=8,CM=2.
BD于点E,BD=8,CM=2.(1)求⊙O的半径;
(2)求证:CE=BE.
分析:(1)可在Rt△OBM中,用半径表示出OM,然后根据勾股定理求出半径的长;
(2)可连接BC,证∠EBC=∠ECB即可;已知的条件是由垂径定理得出的
=
,可有两种证法:
①连接AC,易证得∠CAB=∠BCF,然后根据上面得出的等弧,通过等量代换得出结论;
②将半圆补全,直接由垂径定理求出结果.
(2)可连接BC,证∠EBC=∠ECB即可;已知的条件是由垂径定理得出的
 |
| CD |
 |
| BC |
①连接AC,易证得∠CAB=∠BCF,然后根据上面得出的等弧,通过等量代换得出结论;
②将半圆补全,直接由垂径定理求出结果.
解答:(1)解:∵OC为⊙O的半径,OC⊥BD,
∴DM=MB=
DB;
∵DB=8,∴MB=4(1分)
设⊙O的半径为r,∵CM=2,∴OM=r-2,
在Rt△OMB中,根据勾股定理得(r-2)2+42=r2,
解得r=5;(2分)
(2)证明:
方法一:连接AC、CB,
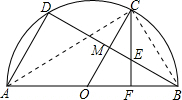 ∵AB是直径,∴∠ACB=90°.
∵AB是直径,∴∠ACB=90°.
∴∠ACF+∠FCB=90°.
又∵CF⊥AB,∴∠CAF+∠ACF=90°
∴∠FCB=∠CAF(3分)∵OC为⊙O的半径,OC⊥BD,
∴C是
的中点,∴∠CAF=∠CBD.(4分)
∴∠FCB=∠DBC.
∴CE=BE;(5分)
方法二:如图,连接BC,补全⊙O,延长CF交⊙O于点G;
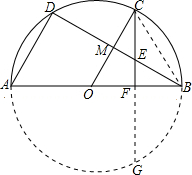 又∵CF⊥AB,AB为直径,
又∵CF⊥AB,AB为直径,
∴
=
.(3分)
∴OC为⊙O的半径,OC⊥BD.
∴C是
的中点,
∴
=
.(4分)
∴
=
.
∴∠FCB=∠DBC.
∴CE=BE.(5分)
∴DM=MB=
| 1 |
| 2 |
∵DB=8,∴MB=4(1分)
设⊙O的半径为r,∵CM=2,∴OM=r-2,
在Rt△OMB中,根据勾股定理得(r-2)2+42=r2,
解得r=5;(2分)
(2)证明:
方法一:连接AC、CB,
 ∵AB是直径,∴∠ACB=90°.
∵AB是直径,∴∠ACB=90°.∴∠ACF+∠FCB=90°.
又∵CF⊥AB,∴∠CAF+∠ACF=90°
∴∠FCB=∠CAF(3分)∵OC为⊙O的半径,OC⊥BD,
∴C是
 |
| BD |
∴∠FCB=∠DBC.
∴CE=BE;(5分)
方法二:如图,连接BC,补全⊙O,延长CF交⊙O于点G;
 又∵CF⊥AB,AB为直径,
又∵CF⊥AB,AB为直径,∴
 |
| BC |
 |
| BG |
∴OC为⊙O的半径,OC⊥BD.
∴C是
 |
| BD |
∴
 |
| BC |
 |
| DC |
∴
 |
| BG |
 |
| DC |
∴∠FCB=∠DBC.
∴CE=BE.(5分)
点评:此题主要考查了圆周角定理、勾股定理以及垂径定理的应用.

练习册系列答案
相关题目
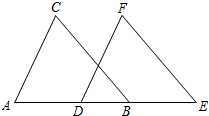 如图,已知点B、D在直线AE上,AC∥DF,∠C=∠F,AD=BE,试说明BC∥EF的理由.
如图,已知点B、D在直线AE上,AC∥DF,∠C=∠F,AD=BE,试说明BC∥EF的理由.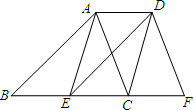 (2013•建邺区一模)如图,已知点E,C在线段BF上,BE=EC=CF,AB∥DE,∠ACB=∠F.
(2013•建邺区一模)如图,已知点E,C在线段BF上,BE=EC=CF,AB∥DE,∠ACB=∠F.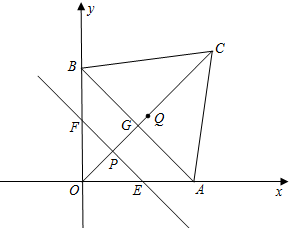 如图,已知点A,B分别在x轴和y轴上,且OA=OB=
如图,已知点A,B分别在x轴和y轴上,且OA=OB=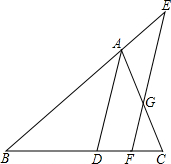 如图,已知点D、F在线段BC上,点E在线段BA的延长线上,EF与AC交于点G,且∠EFC=∠ADC,∠AGE=∠E.请说出AD平分∠BAC的理由.
如图,已知点D、F在线段BC上,点E在线段BA的延长线上,EF与AC交于点G,且∠EFC=∠ADC,∠AGE=∠E.请说出AD平分∠BAC的理由.