Question

已知：如图，⊙O是△ABC的外接圆，∠BAC＝50°，∠ABC＝47°，求∠AOB的度数．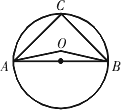

Answer 1

答案：
解析：

分析：要求∠AOB的大小，只要能求出∠C的度数即可，此时的∠C是△ABC的内角，结合已知条件即可求解． 　　解：因为⊙O是△ABC的外接圆，所以∠CAB、∠ABC、∠C都是圆周角，∠AOB是圆心角． 　　又因为∠BAC＝50°，∠ABC＝47°，所以∠C＝180°－(∠BAC＋∠ABC)＝180°－(50°＋47°)＝83°． 　　由圆周角定理，得∠C＝∠AOB． 　　所以∠AOB＝2∠C＝2×83°＝166°． 　　点评：求解此类问题时，一定要正确理解圆周角的概念，掌握圆周角定理．另外，圆周角定理也可以理解成“一条弧所对的圆心角等于它所对的圆周角的二倍．”