题目内容
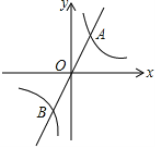
【题目】如图，直线y=mx与双曲线y=
相交于A、B两点，A点的坐标为（1，2）
（1）求反比例函数的表达式；
（2）根据图象直接写出当mx＞时，x的取值范围；
（3）计算线段AB的长．
【答案】（1）反比例函数的表达式是y=
；（2）-1＜x＜0或x＞1；（3）2
．
【解析】
试题分析：（1）把A的坐标代入反比例函数的解析式即可求出答案；
（2）求出直线的解析式，解组成的方程组求出B的坐标，根据A、B的坐标结合图象即可得出答案；
（3）根据A、B的坐标．利用勾股定理分别求出OA、OB，即可得出答案．
试题解析：（1）把A（1，2）代入y=
得：k=2，
即反比例函数的表达式是y=；
（2）把A（1，2）代入y=mx得：m=2，
即直线的解析式是y=2x，
解方程组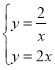
得出B点的坐标是（-1，-2），
∴当mx＞时，x的取值范围是-1＜x＜0或x＞1；
（3）过A作AC⊥x轴于C，
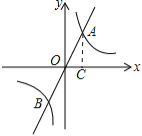
∵A（1，2），
∴AC=2，OC=1，
由勾股定理得：AO=
，
同理求出OB=，
∴AB=2．
练习册系列答案
相关题目
【题目】为了解居民用水情况，在某小区随机抽查了15户家庭的月用水量，结果如下表：
月用水量（吨） | 4 | 5 | 6 | 8 | 9 |
户数 | 2 | 5 | 4 | 3 | 1 |
则这15户家庭的月用水量的众数与中位数分别为（ ）
A.9、6
B.6、6
C.5、6
D.5、5
