题目内容
【题目】如图，已知DB⊥AN于B，交AE于点O，OC⊥AM于点C，且OB=OC，若∠OAB=25°，求∠ADB的度数． 
【答案】解：∵DB⊥AN于B，OC⊥AM于点C，且OB=OC，
∴AE平分∠MAN，
∵∠OAB=25°，
∴∠MAN=50°，
∵DB⊥AN于B，
∴Rt△ABD中，∠ADB=40°．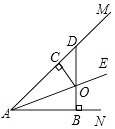
【解析】先根据DB⊥AN于B，OC⊥AM于点C，且OB=OC，得出AE平分∠MAN，再根据∠OAB=25°，得出∠MAN=50°，最后根据DB⊥AN于B，求得∠ADB即可．
【考点精析】本题主要考查了角的平分线和角平分线的性质定理的相关知识点，需要掌握从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线；定理1：在角的平分线上的点到这个角的两边的距离相等； 定理2：一个角的两边的距离相等的点，在这个角的平分线上才能正确解答此题．
练习册系列答案
备战中考寒假系列答案
相关题目
