题目内容
一元二次方程x+3-x(3+x)=0的解为
- A.x1=-3或
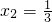
- B.x1=-3或x2=1
- C.x1=-3或x2=-1
- D.x1=3或

B
分析:题目所给的方程,把x+3当作一个整体,方程左边可用提取公因式法,利用因式分解法解方程比较简单.
解答:原方程可变形为:(x+3)(1-x)=0,
x+3=0或1-x=0;
∴x1=-3,x2=1;
故选B.
点评:在用因式分解法解一元二次方程时,一般地要把方程整理为一般式,如果左边的代数式能够分解为两个一次因式的乘积,而右边为零时,则可令每一个一次因式为零,得到两个一元一次方程,解出这两个一元一次方程的解就是原方程的两个解了.
分析:题目所给的方程,把x+3当作一个整体,方程左边可用提取公因式法,利用因式分解法解方程比较简单.
解答:原方程可变形为:(x+3)(1-x)=0,
x+3=0或1-x=0;
∴x1=-3,x2=1;
故选B.
点评:在用因式分解法解一元二次方程时,一般地要把方程整理为一般式,如果左边的代数式能够分解为两个一次因式的乘积,而右边为零时,则可令每一个一次因式为零,得到两个一元一次方程,解出这两个一元一次方程的解就是原方程的两个解了.

练习册系列答案
相关题目
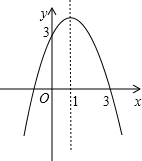 已知二次函数y=-x2+bx+c的图象如图所示,解决下列问题:
已知二次函数y=-x2+bx+c的图象如图所示,解决下列问题: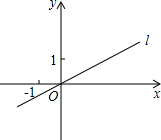 如图,在平面直角坐标系中,直线l的解析式为y=
如图,在平面直角坐标系中,直线l的解析式为y=