题目内容

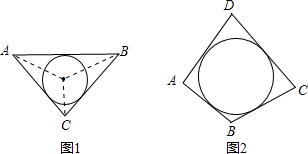阅读材料：如图1，△ABC的周长为l，面积为S，内切圆O的半径为r，探究r与S、l之间的关系．连接OA，OB，OC∵S=S_△OAB+S_△OBC+S_△OCA
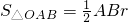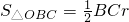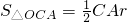
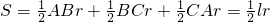
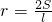
又∵ $数学公式$ ， $数学公式$ ， $数学公式$
∴ $数学公式$
∴ $数学公式$
解决问题：
（1）利用探究的结论，计算边长分别为5，12，13的三角形内切圆半径；
（2）若四边形ABCD存在内切圆（与各边都相切的圆），如图2且面积为S，各边长分别为a，b，c，d，试推导四边形的内切圆半径公式；
（3）若一个n边形（n为不小于3的整数）存在内切圆，且面积为S，各边长分别为a₁，a₂，a₃，…，a_n，合理猜想其内切圆半径公式（不需说明理由）．

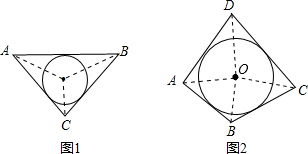解：（1）∵5²+12²=13²，
∴三角形为直角三角形
面积 $\text{[math]}$ ，
∴ $\text{[math]}$ ；

（2）设四边形ABCD内切圆的圆心为O，连接OA，OB，OC，OD，
则S=S_△OAB+S_△OBC+S_△OCD+S_△ODA= $\text{[math]}$ = $\text{[math]}$ （a+b+c+d）•r，
∴ $\text{[math]}$ ；

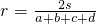（3）类比（1）（2）的结论，
易得在圆内切n边形中，有 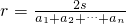$\text{[math]}$ 成立．
分析：（1）根据题意，易得边长分别为5，12，13的三角形为直角三角形，进而由直角三角形的性质可得答案；
（2）设四边形ABCD内切圆的圆心为O，连接OA，OB，OC，OD，类比阅读材料，可得S=S_△OAB+S_△OBC+S_△OCA+S_△ODA，进而可得答案；
（3）由（1）（2）的结论，类比分析可得答案．
点评：本题考查学生根据阅读材料，结合课本的知识，分析、解决问题的能力．

练习册系列答案

尖子生培优教材系列答案

走进重高培优讲义系列答案

孟建平系列一课三练课时导学系列答案

激活课堂课时作业系列答案

优等生题库系列答案

亮点激活教材多元演练系列答案

小助手高效课时学案系列答案

金质课堂系列答案

初中同步学习导与练导学探究案系列答案

金版课堂系列答案

相关题目

25、阅读材料：
如图（一），在已建立直角坐标系的方格纸中，图形①的顶点为A、B、C，要将它变换到图④（变换过程中图形的顶点必须在格点上，且不能超出方格纸的边界）．
例如：将图形①作如下变换（如图二）．
第一步：平移，使点C（6，6）移至点（4，3），得图②；
第二步：旋转，绕着点（4，3）旋转180°，得图③；
第三步：平移，使点（4，3）移至点O（0，0），得图④．
则图形①被变换到了图④．

解决问题：
（1）在上述变化过程中A点的坐标依次为：
（4，6）→（

）
（2）如图（三），仿照例题格式，在直角坐标系的方格纸中将△DEF经过平移、旋转、翻折等变换得到△OPQ．（写出变换步骤，并画出相应的图形）

阅读材料：
如图1，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”（a），中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高（h）”．我们可得出一种计算三角形面积的新方法：S△ABC=

ah，即三角形面积等于水平宽与铅垂高乘积的一半．
解答下列问题：

如图2，抛物线顶点坐标为点C（-1，-4），交x轴于点A（-3，0），交y轴于点B．
（1）求抛物线和直线AB的解析式；
（2）点P是抛物线（在第三象限内）上的一个动点，连接PA，PB，当P点运动到顶点C时，求△CAB的铅垂高CD及S_△CAB；
（3）是否存在一点P，使S_△PAB=S_△CAB，若存在，求出P点的坐标；若不存在，请说明理由．

（2013•益阳）阅读材料：如图1，在平面直角坐标系中，A、B两点的坐标分别为A（x₁，y₁），B（x₂，y₂），AB中点P的坐标为（x_p，y_p）．由x_p-x₁=x₂-x_p，得x_p=

，所以AB的中点坐标为(

)．由勾股定理得AB²=

x2-	x1

y2-	y1

2，所以A、B两点间的距离公式为AB=

(x2-x1)2+(y2-y1)2

．
注：上述公式对A、B在平面直角坐标系中其它位置也成立．
解答下列问题：
如图2，直线l：y=2x+2与抛物线y=2x²交于A、B两点，P为AB的中点，过P作x轴的垂线交抛物线于点C．
（1）求A、B两点的坐标及C点的坐标；
（2）连结AB、AC，求证△ABC为直角三角形；
（3）将直线l平移到C点时得到直线l′，求两直线l与l′的距离．

阅读材料：如图，AB=AC，BD=CD，则可证得AD平分∠BAC，据此我们引出了“角平分线”的尺规作法．

问题：如图，AD=AE，AB=AC，也可证得AP平分∠BAC，据此我们能否引出了“角平分线”的第二种尺规作法呢？请在图中尝试着画出∠α的平分线．

阅读材料：

如图1，AB、CD交于点O，我们把△AOD和△BOC叫做对顶三角形．
结论：若△AOD和△BOC是对顶三角形，则∠A+∠D=∠B+∠C．
结论应用举例：
如图2：求五角星的五个内角之和，即∠A+∠B+∠ACE+∠ADB+∠E的度数．
解：连接CD，由对顶三角形的性质得：∠B+∠E=∠1+∠2，
在△ACD中，∵∠A+∠ACD+∠ADC=180°，
即∠A+∠3+∠1+∠2+∠4=180°，
∴∠A+∠ACE+∠B+∠E+ADB=180°
即五角星的五个内角之和为180°．
解决问题：
（1）如图①，∠A+∠B+∠C+∠D+∠E+∠F=

；
（2）如图②，∠A+∠B+∠C+∠D+∠E+∠F+∠G=

；
（3）如图③，∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=

；
（4）如图④，∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=

；
请你从图③或图④中任选一个，写出你的计算过程．