题目内容
(2013•益阳)阅读材料:如图1,在平面直角坐标系中,A、B两点的坐标分别为A(x1,y1),B(x2,y2),AB中点P的坐标为(xp,yp).由xp-x1=x2-xp,得xp=
,同理yp=
,所以AB的中点坐标为(
,
).由勾股定理得AB2=
2+
2,所以A、B两点间的距离公式为AB=
.
注:上述公式对A、B在平面直角坐标系中其它位置也成立.
解答下列问题:
如图2,直线l:y=2x+2与抛物线y=2x2交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.
(1)求A、B两点的坐标及C点的坐标;
(2)连结AB、AC,求证△ABC为直角三角形;
(3)将直线l平移到C点时得到直线l′,求两直线l与l′的距离.

| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
|
|
| (x2-x1)2+(y2-y1)2 |
注:上述公式对A、B在平面直角坐标系中其它位置也成立.
解答下列问题:
如图2,直线l:y=2x+2与抛物线y=2x2交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.
(1)求A、B两点的坐标及C点的坐标;
(2)连结AB、AC,求证△ABC为直角三角形;
(3)将直线l平移到C点时得到直线l′,求两直线l与l′的距离.

分析:(1)根据y=2x+2与抛物线y=2x2交于A、B两点,直接联立求出交点坐标,进而得出C点坐标即可;
(2)利用两点间距离公式得出AB的长,进而得出PC=PA=PB,求出∠PAC+∠PCB=90°,即∠ACB=90°即可得出答案;
(3)点C作CG⊥AB于G,过点A作AH⊥PC于H,利用A,C点坐标得出H点坐标,进而得出CG=AH,求出即可.
(2)利用两点间距离公式得出AB的长,进而得出PC=PA=PB,求出∠PAC+∠PCB=90°,即∠ACB=90°即可得出答案;
(3)点C作CG⊥AB于G,过点A作AH⊥PC于H,利用A,C点坐标得出H点坐标,进而得出CG=AH,求出即可.
解答: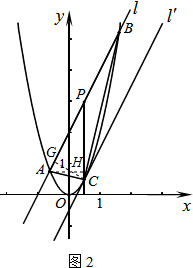 (1)解:由
(1)解:由
,
解得:
,
.
则A,B两点的坐标分别为:A(
,3-
),B(
,3+
),
∵P是A,B的中点,由中点坐标公式得P点坐标为(
,
),即(
,3),
又∵PC⊥x轴交抛物线于C点,将x=
代入y=2x2中得y=
,
∴C点坐标为(
,
).
(2)证明:由两点间距离公式得:
AB=
=5,PC=|3-
|=
,
∴PC=PA=PB,
∴∠PAC=∠PCA,∠PBC=∠PCB,
∴∠PAC+∠PCB=90°,即∠ACB=90°,
∴△ABC为直角三角形.
(3)解:过点C作CG⊥AB于G,过点A作AH⊥PC于H,
则H点的坐标为(
,3-
),
∴S△PAC=
AP•CG=
PC•AH,
∴CG=AH=|
-
|=
.
又直线l与l′之间的距离等于点C到l的距离CG,
∴直线l与l′之间的距离为
.
 (1)解:由
(1)解:由
|
解得:
|
|
则A,B两点的坐标分别为:A(
1-
| ||
| 2 |
| 5 |
1+
| ||
| 2 |
| 5 |
∵P是A,B的中点,由中点坐标公式得P点坐标为(
| ||||||||
| 2 |
3-
| ||||
| 2 |
| 1 |
| 2 |
又∵PC⊥x轴交抛物线于C点,将x=
| 1 |
| 2 |
| 1 |
| 2 |
∴C点坐标为(
| 1 |
| 2 |
| 1 |
| 2 |
(2)证明:由两点间距离公式得:
AB=
(
|
| 1 |
| 2 |
| 5 |
| 2 |
∴PC=PA=PB,
∴∠PAC=∠PCA,∠PBC=∠PCB,
∴∠PAC+∠PCB=90°,即∠ACB=90°,
∴△ABC为直角三角形.
(3)解:过点C作CG⊥AB于G,过点A作AH⊥PC于H,
则H点的坐标为(
| 1 |
| 2 |
| 5 |
∴S△PAC=
| 1 |
| 2 |
| 1 |
| 2 |
∴CG=AH=|
1-
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
又直线l与l′之间的距离等于点C到l的距离CG,
∴直线l与l′之间的距离为
| ||
| 2 |
点评:此题主要考查了二次函数的综合应用以及两点之间距离公式和两函数交点坐标求法等知识,根据数形结合得出H点坐标是解题关键.

练习册系列答案
相关题目