题目内容
【题目】在△ABC中,∠B=22.5°,∠C=30°,AB的垂直平分线OD交BC边于点D,连结AD
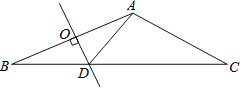
(1)求∠DAC的度数;
(2)若AC=4cm,求△ABC的面积(结果保留根号)
【答案】(1)∠DAC=105°;(2)![]()
【解析】
试题分析:(1)根据线段的垂直平分线的性质得到AD=BD,得到∠B=∠BAD=22.5°,根据三角形外角的性质求出∠ADC=45°,根据三角形内角和定理计算即可;
(2)过A点作AE⊥BC于点E,则AE=DE,根据直角三角形的性质求出AE、BC的长,根据三角形面积公式计算即可.
解:(1)∵OD是AB的垂直平分线;
∴AD=BD,
∴∠B=∠BAD=22.50,
∴∠ADC=45°,
∵∠A=30°,
∴∠DAC=105°;
(2)过A点作AE⊥BC于点E,则AE=DE,
在Rt△ACE中,
∵AC=4,
∴AE=2,EC=2![]() ,
,
∴DE=2,
在Rt△AED中,
AD=2![]() ,
,
∴AD=BD=2![]() ,
,
∴BC=2![]() +2
+2![]() +2
+2
∴S△ABC=![]() =
=![]() (
(![]() )=(
)=(![]() ).
).


练习册系列答案
相关题目
【题目】正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
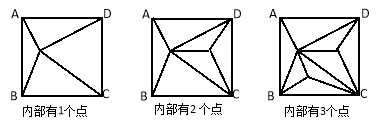
(1)填写下表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 4 | 6 | … |
(2)原正方形能否被分割成2016个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.