题目内容
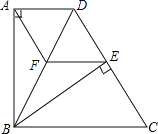
【题目】如图本题图①,在等腰Rt![]() 中,
中,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点,以
上一点,以![]() 为半径作
为半径作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,线段
,线段![]() 、
、![]() 、
、![]() 的中点分别为
的中点分别为![]() 、
、![]() 、
、![]() .
.
(1)试探究![]() 是什么特殊三角形?说明理由;
是什么特殊三角形?说明理由;
(2)将![]() 绕点
绕点![]() 逆时针方向旋转到图②的位置,上述结论是否成立?并证明结论;
逆时针方向旋转到图②的位置,上述结论是否成立?并证明结论;
(3)若![]() ,把
,把![]() 绕点
绕点![]() 在平面内自由旋转,求
在平面内自由旋转,求![]() 的面积y的最大值与最小值的差.
的面积y的最大值与最小值的差.
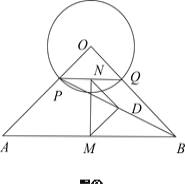
【答案】(1)![]() 为等腰直角三角形;(2)
为等腰直角三角形;(2)![]() 仍然为等腰直角三角形;(3)
仍然为等腰直角三角形;(3)![]() 的最大值与最小值的差为:
的最大值与最小值的差为:![]()
【解析】分析:(1)由OA=OB,OP=OQ可得AP=BQ,再利用三角形的中位线可得△DMN是等腰直角三角形;
(2)由旋转的性质得∠AOP=∠BOQ,从而可证△AOP≌△BOQ,由三角形中位线的性质可得DM=DN,根据平行线的性质和三角形内角和可证∠MDN=90°,从而结论得证;
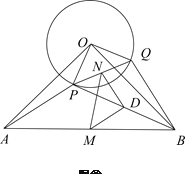
(3)如图,设⊙![]() 交
交![]() 于点
于点![]() ,交
,交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .由三角形三边的关系得
.由三角形三边的关系得![]() ,
,![]() ,由三角形的面积公式得
,由三角形的面积公式得![]() ,从而可求出y的最大值和最小值,然后相减即可.
,从而可求出y的最大值和最小值,然后相减即可.
详解:(1)![]() 为等腰直角三角形
为等腰直角三角形
![]()
![]() 分别为
分别为![]() 的中点,
的中点,
![]()
![]() 且
且![]()
同理:![]()
![]()
![]()
![]()
![]() .
.
又![]()
![]()
![]()
![]() 即
即![]() 为等腰直角三角形.
为等腰直角三角形.
(2)如图,![]() 仍然为等腰直角三角形.
仍然为等腰直角三角形.
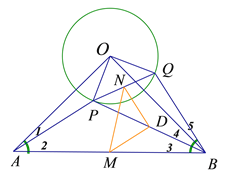
证明:由旋转的性质,![]() .
.
![]()
![]()
![]()
![]() ≌
≌![]() ,
,
![]()
![]() .
.
![]()
![]() 分别为
分别为![]() 的中点,
的中点,![]()
![]() 且
且![]()
同理:![]() ,
,![]()
![]()
在等腰Rt![]() 中,
中,![]()
![]()
![]()
![]()
![]()
![]()
![]() 同理:
同理:![]()
![]()
![]()
=![]()
![]() .
.
![]()
![]()
![]()
![]() 为等腰直角三角形.
为等腰直角三角形.
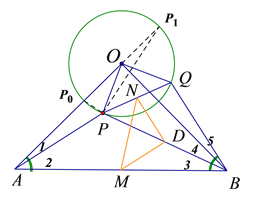
(3), 如图,设⊙![]() 交
交![]() 于点
于点![]() ,交
,交![]() 延长线于点
延长线于点![]() ,
,
连接![]()
![]() ,而
,而![]() ,
,
![]() 同理,
同理,![]()
由题意,![]() ,
,
![]()
![]() 的最小值为
的最小值为![]() . 同理,
. 同理,![]() 最大值为
最大值为![]() ,
,
从而得![]() 的最大值与最小值的差为:
的最大值与最小值的差为:![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】用火柴棒按下列方式搭建三角形:
![]()
三角形个数 | 1 | 2 | 3 | 4 | … |
火柴棒根数 | 3 | 5 | 7 | 9 | … |
(1)当三角形的个数为n时,火柴棒的根数是多少?
(2)求当n=100时,有多少根火柴棒?
(3)当火柴棒的根数为2017时,三角形的个数是多少?