题目内容
已知抛物线y=ax2+bx+c与直线y=mx+n相交于两点,这两点的坐标分别是(0,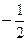 )和
)和 (m-b,m2-mb+n),其中a,b,c
(m-b,m2-mb+n),其中a,b,c ,m,n为实数,且a,m不为0.
,m,n为实数,且a,m不为0.
(1)求c的值;
(2)设抛物线y=ax2+bx+c与x轴的两个交点是(x1,0)和(x2,0),求x1x2的值;
(3)当-1≤x≤1时,设抛物线y=ax2+bx+c上与x轴距离最大的点为P(xo,yo ),求这时|yo|的最小值.
解:
(1)∵(0,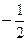 )在y=ax2+bx+c上,∴
)在y=ax2+bx+c上,∴ 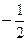 =a×02+b×0+c, ∴ c=
=a×02+b×0+c, ∴ c=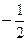 .(1分)
.(1分)
(2)又可得 n=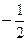 .
.
∵ 点(m-b,m2-mb+n)在y=ax2+bx+c上,
∴ m2-mb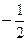 =a(m-b)2+b(m-b)
=a(m-b)2+b(m-b)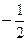 ,
,
∴(a-1)(m-b)2=0, (2分)
若(m-b)=0,则(m-b, m2-mb+n)与(0,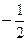 )重合,与题意不合.
)重合,与题意不合.
∴ a=1.(3分,只要求出a=1,即评3分)
∴抛物线y=ax2+bx+c,就是y=x2+bx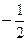 .
.
△=b2-4ac=b2-4×(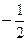 )>0,(没
)>0,(没 写出不扣分)
写出不扣分)
∴抛物线y=ax2+bx+c与x轴的两个交点的横坐标就是关于x的二次方程0=ax2+bx+c的两个实数根,∴由根与系数的关系,得x1x2=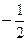 . (4分)
. (4分)
(3)抛物线y=x2+bx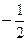 的对称轴为x=
的对称轴为x= ,最小值为
,最小值为 .(没写出不扣分)
.(没写出不扣分)
设抛物线y=x2+bx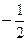 在x轴上方与x轴距离最大的点的纵坐标为H,在x轴下方与x轴距离最大的点的纵坐标为h.
在x轴上方与x轴距离最大的点的纵坐标为H,在x轴下方与x轴距离最大的点的纵坐标为h.
①当 <-1,即b>2时,在x轴上方与x轴距离最大的点是(
<-1,即b>2时,在x轴上方与x轴距离最大的点是( 1,yo),
1,yo),
∴|H|=yo=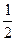 +b>
+b> , (5分)
, (5分)
在x轴下方与x轴距离最大的点是(-1,yo),
∴|h|=|yo|=|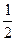 -b|=b-
-b|=b-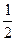 >
>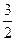 , (6分)
, (6分)
∴|H|>|h|.∴这时|yo|的最小值大于 . (7分)
. (7分)
② 当-1≤ ≤0,即0≤b≤2时,
≤0,即0≤b≤2时,
在x轴上方与x轴距离最大的点是(1,yo),
∴|H|=yo=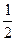 +b≥
+b≥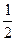 ,当b=0时等号成立.
,当b=0时等号成立.
在x轴下方与x轴距离最大点的是 ( ,
, ),
),
∴|h|=| |=
|=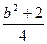 ≥
≥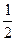 ,当b=0时等号成立.
,当b=0时等号成立.
∴这时|yo|的最小值等于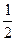 . (8分)
. (8分)
③ 当0 <
< ≤1,即-2≤b<0时,
≤1,即-2≤b<0时,
在x轴上方与x轴距离最大的点是(-1,yo),
∴|H|=yo=|1+(-1)b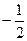 |=|
|=|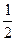 -b|=
-b|=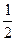 -b>
-b>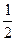
在x轴下方与x轴距离最大的点是 ( ,
, ),
),
∴|h|=|yo|=| |=
|=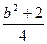 >
>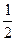 .
.
∴ 这 时 |yo|的 最 小 值 大 于 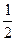 . (9分)
. (9分)
④ 当1< ,即b<-2时,
,即b<-2时,
在x轴上方与x轴距离最大的点是(-1,yo),∴|H|=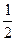 -b>
-b> ,
,
在x轴下方与x轴距离最大的点是(1,yo),∴|h|=|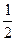 +b|=-(b+
+b|=-(b+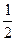 )>
)>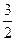 ,
,
∴|H|>|h|,∴这时|y o|的最小值大于
o|的最小值大于 . (10分)
. (10分)
综上所述,当b=0,x0=0时,这时|yo|取最小值,为|yo|=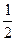 . (11分)
. (11分)
解析

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 (3)在(2)的结论下,直线x=1上是否存在点M,使△MPQ为等腰三角形?若存在,请求出所有点M的坐
(3)在(2)的结论下,直线x=1上是否存在点M,使△MPQ为等腰三角形?若存在,请求出所有点M的坐 (3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90°的点P的坐标.
(3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90°的点P的坐标.

 轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;
轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;