题目内容
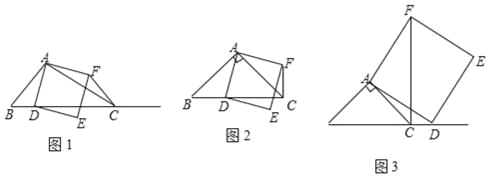
【题目】已知如图:△ABC中,∠B、∠C的平分线相交于点O,过点O作EF∥BC交AB、AC于E、F.
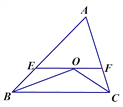
(1)图中有几个等腰三角形?试说明理由,并请指出EF与BE、CF间有怎样的关系?
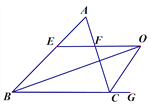
(2)若△ABC中,∠B的平分线与三角形外角∠ACG的平分线CO交于点O,过O点作OE∥BC交AB于E,交AC于F(如图2),请直接写出EF与BE、CF间的关系,不用证明.
【答案】(1)有2个等腰三角形分别是:等腰△OBE和等腰△OCF;(2)EF=BE-CF
【解析】试题分析:(1)根据角平分线的定义可得: ∠EBO=∠CBO,∠FCO=∠BCO,根据两直线平行内错角相等的性质可得:∠EOB=∠CBO,∠FOC=∠BCO,等量代换可得:∠EBO=∠EOB,∠FCO=∠FOC,利用等角对等边可判定:BE=EO,FO=CF,所以△OBE和△OCF是等腰三角形,又因为EF=OE+OF,所以EF=BE+CF,
(2) 根据角平分线的定义可得: ∠EBO=∠CBO,∠FCO=∠OCG,根据两直线平行内错角相等的性质可得:∠EOB=∠CBO,∠FOC=∠OCG,等量代换可得:∠EBO=∠EOB,∠FCO=∠FOC,利用等角对等边可判定:BE=EO,FO=CF,所以△OBE和△OCF是等腰三角形,又因为EF=OE-OF,所以EF=BE-CF.
试题解析:(1)有2个等腰三角形分别是:等腰△OBE和等腰△OCF,
理由如下:OB平分∠ABC,
∴∠ABO=∠OBC,
∵EF∥BC,
∴∠EOB=∠OBC,
∴∠ABO=∠EOB,
∴EO=EB,
∴△OBE是等腰三角形,
同理FO=FC,△OCF是等腰三角形,
∴EF=OE+OF=BE+CF,
(2)EF=BE-CF.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目