题目内容
【题目】如图,在等腰![]() 中,
中, ![]() ,
, ![]() 是斜边上
是斜边上![]() 上任一点,
上任一点, ![]() 于
于![]() ,
, ![]() 交
交![]() 的延长线于
的延长线于![]() ,
, ![]() 于点
于点![]() ,交
,交![]() 于
于![]() .
.
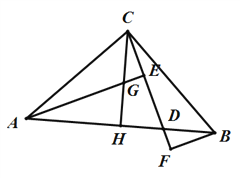
(1)求证: ![]() .
.
(2)探索![]() 与
与![]() 、
、![]() 之间的数量关系.
之间的数量关系.
【答案】(1)证明见解析;(2)AE=EF+BF,理由见解析.
【解析】试题分析:(1)根据等腰直角三角形的性质和全等三角形的判定ASA和性质可证明;
(2)通过全等三角形的判定AAS证明△ACE≌△CBF,然后根据全等的性质可求得关系.
试题解析:(1)∵ABC为等腰直角三角形,且CH⊥AB
∴∠ACG=45°
∵∠CAG+∠ACE=90°,∠BCF+∠ACE=90°
∴∠CAG=∠BCF
在△ACG和△CBD中
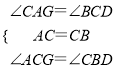
∴△ACG≌△CBD(ASA)
∴BD=CG
(2)AE=EF+BF
理由如下:
在△ACE和△CBF中,

∴△ACE≌△CBF,
∴AE=CF,CE=BF,
∴AE=CF=CE+EF=BF+EF.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某班学生在颁奖大会上得知该班获得奖励的情况如下表:已知该班共有28人获得奖励,其中只获得两项奖励的有13人,那么该班获得奖励最多的一位同学可能获得的奖励为( )
项目 | 三好学生 | 优秀学生干部 | 优秀团员 |
市级 | 3 | 2 | 3 |
校级 | 18 | 6 | 12 |
A.3项
B.4项
C.5项
D.6项