题目内容
菱形ABCD的边长为5，两条对角线交于点O，且AO、BO的长分别是关于x的方程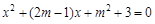
两根，求m的值．
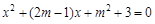两根，求m的值．
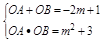，∵四边形ABCD为菱形，∴OA⊥OB，有
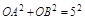
代入整理得
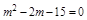解之得
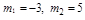（此时方程无实数根故舍去）∴
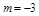
由题意可知：菱形ABCD的边长是5，则AO2+BO2=25，则再根据根与系数的关系可得：AO+BO=-2m+1，AO?BO=m2+3；代入AO2+BO2中，得到关于m的方程后，求得m的值．
解：由勾股定理可得：AO2+BO2=25，
又有根与系数的关系可得：AO+BO=-2m+1，AO?BO=m2+3
∴AO2+BO2=（AO+BO）2-2AO?BO=（-2m+1）2-2（m2+3）=25，
整理得：m2-2m-15=0，
解得：m=-3或5．
又∵△＞0，∴（2m-1）2-4（m2+3）＞0，解得m＜-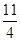
，
∴m=-3，
解：由勾股定理可得：AO2+BO2=25，
又有根与系数的关系可得：AO+BO=-2m+1，AO?BO=m2+3
∴AO2+BO2=（AO+BO）2-2AO?BO=（-2m+1）2-2（m2+3）=25，
整理得：m2-2m-15=0，
解得：m=-3或5．
又∵△＞0，∴（2m-1）2-4（m2+3）＞0，解得m＜-
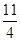，∴m=-3，
练习册系列答案
相关题目
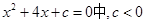，该方程根的情况是
的一元二次方程
的两个实数根是
，且
，则
的值是（ ）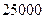
元的均价对外销售，由于国务院有关房地产的新政策出台，购房者持币观望．为了加快资金周转，房地产开发商对价格进行两次下调，最终以每平方米
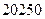元的均价开盘销售．
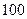平方米的房子．开发商还给予以下两种优惠方案以供选择：①一次付清全款打九九折；②一次付清全款不打折，送五年物业管理费．如该楼盘物业管理费是每月
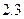元/米2．请问哪种方案更优惠？
。
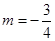时，求方程的正根．