题目内容
(2012•淄博)如图,将正方形对折后展开(图④是连续两次对折后再展开),再按图示方法折叠,能够得到一个直角三角形,且它的一条直角边等于斜边的一半.这样的图形有( )
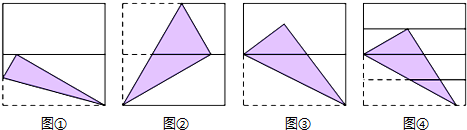

分析:根据含30°角所对的直角边等于斜边一半,然后依次判断直角三角形中能否找到一个角等于30°,从而判断出答案.
解答:解: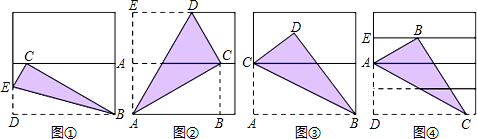
设正方形的边长为a,
在图①中,AB=
a,BC=DB=a,
故∠ACB=30°,∠ABC=60°,
故可得∠CBE=∠DBE=15°,故不能满足它的一条直角边等于斜边的一半.
在图②中,BC=
a,AC=AE=a,
故∠BAC=30°,
从而可得∠CAD=∠EAD=30°,故能满足它的一条直角边等于斜边的一半.
在图③中,AC=
a,AB=a,
故∠ABC=∠DBC≠30°,故不能满足它的一条直角边等于斜边的一半.
在图④中,AE=
a,AB=AD=
a,
故∠ABE=30°,∠EAB=60°,
从而可得∠BAC=∠DAC=60°,∠ACB=30°,故能满足它的一条直角边等于斜边的一半.
综上可得有2个满足条件.
故选C.

设正方形的边长为a,
在图①中,AB=
| 1 |
| 2 |
故∠ACB=30°,∠ABC=60°,
故可得∠CBE=∠DBE=15°,故不能满足它的一条直角边等于斜边的一半.
在图②中,BC=
| 1 |
| 2 |
故∠BAC=30°,
从而可得∠CAD=∠EAD=30°,故能满足它的一条直角边等于斜边的一半.
在图③中,AC=
| 1 |
| 2 |
故∠ABC=∠DBC≠30°,故不能满足它的一条直角边等于斜边的一半.
在图④中,AE=
| 1 |
| 4 |
| 1 |
| 2 |
故∠ABE=30°,∠EAB=60°,
从而可得∠BAC=∠DAC=60°,∠ACB=30°,故能满足它的一条直角边等于斜边的一半.
综上可得有2个满足条件.
故选C.
点评:此题主要考查了直角三角形的性质,等边三角形的判定及图形折叠等知识的综合应用能力及推理能力,难度较大,注意细心、耐心思考.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
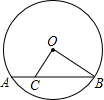 (2012•淄博)如图,⊙O的半径为2,弦AB=
(2012•淄博)如图,⊙O的半径为2,弦AB= (2012•淄博)如图,正方形AOCB的边长为4,反比例函数的图象过点E(3,4).
(2012•淄博)如图,正方形AOCB的边长为4,反比例函数的图象过点E(3,4). (2012•淄博)如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则
(2012•淄博)如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则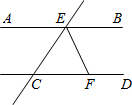 (2012•淄博)如图,AB∥CD,CE交AB于点E,EF平分∠BEC,交CD于F.若∠ECF=40°,则∠CFE=
(2012•淄博)如图,AB∥CD,CE交AB于点E,EF平分∠BEC,交CD于F.若∠ECF=40°,则∠CFE=