题目内容
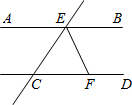 (2012•淄博)如图,AB∥CD,CE交AB于点E,EF平分∠BEC,交CD于F.若∠ECF=40°,则∠CFE=
(2012•淄博)如图,AB∥CD,CE交AB于点E,EF平分∠BEC,交CD于F.若∠ECF=40°,则∠CFE=70
70
度.分析:先根据平行线的性质得出∠AEC的度数,再由平角的性质及角平分线的定义求出∠CEF的度数,根据三角形内角和定理即可得出结论.
解答:解:∵AB∥CD,∠ECF=40°,
∴∠AEC=∠ECF=40°,
∴∠BEC=180°-∠AEC=180°-40°=140°,
∵EF平分∠BEC,
∴∠CEF=
∠BEC=
×140°=70°,
∴∠CFE=180°-∠ECF-∠CEF=180°-40°-70°=70°.
故答案为:70.
∴∠AEC=∠ECF=40°,
∴∠BEC=180°-∠AEC=180°-40°=140°,
∵EF平分∠BEC,
∴∠CEF=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠CFE=180°-∠ECF-∠CEF=180°-40°-70°=70°.
故答案为:70.
点评:本题考查的是平行线的性质,在解答此类题目时往往用到三角形的内角和是180°这一隐藏条件.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
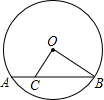 (2012•淄博)如图,⊙O的半径为2,弦AB=
(2012•淄博)如图,⊙O的半径为2,弦AB= (2012•淄博)如图,正方形AOCB的边长为4,反比例函数的图象过点E(3,4).
(2012•淄博)如图,正方形AOCB的边长为4,反比例函数的图象过点E(3,4).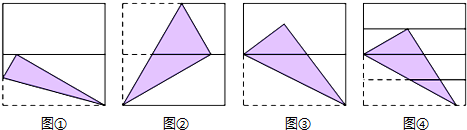
 (2012•淄博)如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则
(2012•淄博)如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则