题目内容
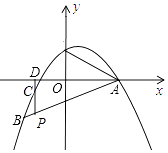
【题目】如图，正△ABC的边长为2，以BC边上的高AB1为边作正△AB1C1 ， △ABC与△AB1C1公共部分的面积记为S1；再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2 ， △AB1C1与△AB2C2公共部分的面积记为S2；…，以此类推，那么S3= ， 则Sn= ． （用含n的式子表示） 
【答案】
（ 
）3； （ ）n
【解析】解：∵等边三角形ABC的边长为2，AB1⊥BC， ∴BB1=1，AB=2，
根据勾股定理得：AB1= 
，
∴S1= 
× 
×（ ）2= （ ）1；
∵等边三角形AB1C1的边长为 ，AB2⊥B1C1 ，
∴B1B2= ，AB1= ，
根据勾股定理得：AB2= 
，
∴S2= × ×（ ）2= （ ）2；
依此类推，Sn= （ ）n；
∴S3= （ ）3 ，
故答案为： （ ）3 ， （ ）n ．
由AB1为边长为2的等边三角形ABC的高，利用三线合一得到B1为BC的中点，求出BB1的长，利用勾股定理求出AB1的长，进而求出S1 ， 同理求出S2 ， 依此类推，得到Sn ．
练习册系列答案
相关题目
【题目】九年级（3）班数学兴趣小组经过市场调查整理出某种商品在第x天（1≤x≤90，且x为整数）的售价与销售量的相关信息如下．已知商品的进价为30元/件，设该商品的售价为y（单位：元/件），每天的销售量为p（单位：件），每天的销售利润为w（单位：元）．
时间x（天） | 1 | 30 | 60 | 90 |
每天销售量p（件） | 198 | 140 | 80 | 20 |
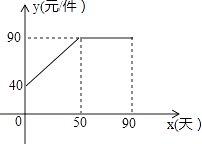
（1）求出w与x的函数关系式；
（2）问销售该商品第几天时，当天的销售利润最大？并求出最大利润；
（3）该商品在销售过程中，共有多少天每天的销售利润不低于5600元？请直接写出结果．
