题目内容
【题目】如图,在等腰梯形ABCD中,AC⊥BD,AC=6cm,则等腰梯形ABCD的面积为cm2 . 
【答案】18
【解析】解:方法一:
过点B作BE∥AC,交DC的延长线于点E,又AB∥CE,
∴四边形ACEB是平行四边形,又等腰梯形ABCD
∴BE=AC=DB=6cm,AB=CE,
∵AC⊥BD,
∴BE⊥BD,
∴△DBE是等腰直角三角形,
∴S等腰梯形ABCD= ![]() =
= ![]() =
= ![]() =S△DBE=
=S△DBE= ![]()
=6×6÷2
=18(cm2).
方法二:
∵BD是△ADB和△CDB的公共底边,又AC⊥BD,
∴AC=△ADB的高﹢△CDB的高,
∴梯形ABCD的面积=△ADB面积+△CDB面积= ![]() BD×AC=6×
BD×AC=6× ![]() =18(cm2).
=18(cm2).
所以答案是:18.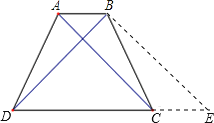
【考点精析】利用等腰梯形的性质对题目进行判断即可得到答案,需要熟知等腰梯形的两腰相等;同一底上的两个角相等;两条对角线相等.

练习册系列答案
相关题目