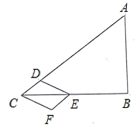
题目内容
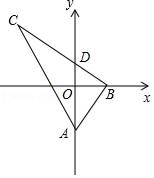
【题目】如图，在
中，
，
，
．动点
从点
出发，沿线段
向终点
以
/
的速度运动，同时动点
从点出发，沿折线
以
/的速度向终点运动，当有一点到达终点时，另一点也停止运动，以
、
为邻边作设
与重叠部分图形的面积为
点运动的时间为
．
（1）当点在
边上时，求
的长（用含
的代数式表示）；
（2）当点
落在线段
上时，求
的值；
（3）求
与之间的函数关系式
，并写出自变量的取值范围．
【答案】（1）
；（2）
；（3）详见解析
【解析】
（1）根据动点
从点
出发，沿折线
以
/
的速度向终点
运动，得出
，即可表达出AE的表达式；
（2）由
，可得
，可得
，列出方程即可求解；
（3））分当
时，当
时，当
时，三种情况进行画图解答即可．
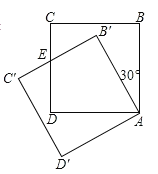
解：（1）当点在
边上时,,
∴
∴．
（2）如图：当点
落在线段
上时，此时：
在
中，
，
，
∴
∴
在
中：，
，
，
，
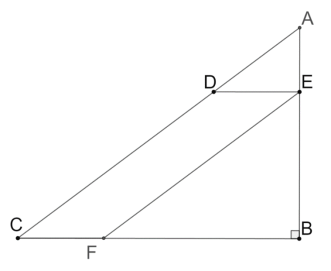
解得．
（3）依题意得：
在中，，，
∴
∴
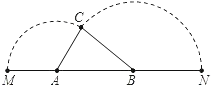
当时，此时E在CB边上，此时
如图：过D作DM⊥BC于M
∴
∵
∴
∴
∴
∴
∴
∴
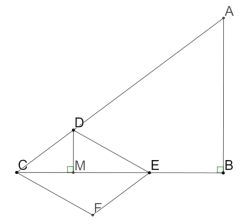
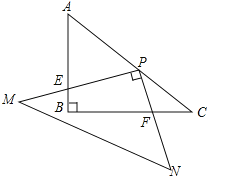
当时，E在AB边上，F在BC的下方，此时：
如图：过E作EP⊥AC于E, EF交BC于Q,连接CE
∴
∴
∵
∴
∴
∴
∴
∴
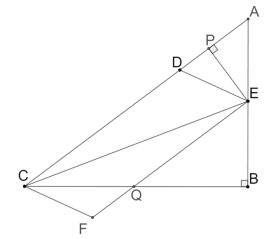
在中EQ//AC
∴
∴
∴
∴
∴
当时，E在AB边上，F在BC的上方，此时：
如图：过E作EP⊥AC于E,
∴
∴
∵
∴
∴
∴
∴
∴
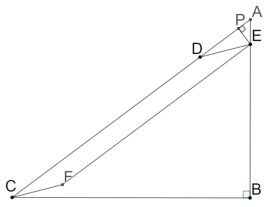
∴综上所述：
与
之间的函数关系式是：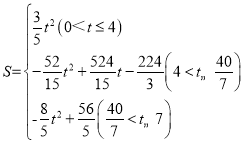
练习册系列答案
相关题目
【题目】在如图中，每个正方形有边长为1 的小正方形组成：
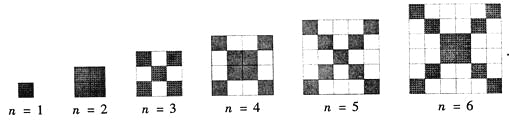
（1） 观察图形，请填写下列表格：
正方形边长 | 1 | 3 | 5 | 7 | … | n(奇数) |
黑色小正方形个数 | … | |||||
正方形边长 | 2 | 4 | 6 | 8 | … | n(偶数) |
黑色小正方形个数 | … |
（2）在边长为n（n≥1）的正方形中，设黑色小正方形的个数为P1，白色小正方形的个数为P2，问是否存在偶数n，使P2＝5P1？若存在，请写出n的值；若不存在，请说明理由.
