Question

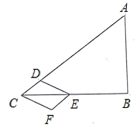
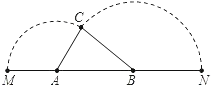
【题目】已知A、B是线段MN上的两点，MN=4，MA=1，MB＞1．以A为中心顺时针旋转点M，以B为中心逆时针旋转点N，使M、N两点重合成一点C，构成△ABC．设AB=x，请解答：（1）x的取值范围______；

（2）若△ABC是直角三角形，则x的值是______．

Answer 1

【答案】1＜x＜2 x或x．

【解析】

（1）因为所求AB或x在△ABC中，所以可利用三角形三边之间的关系即两边之和大于第三边，两边之差小于第三边进行解答．

（2）应该分情况讨论，因为不知道在三角形中哪一个是作为斜边存在的．所以有三种情况，即：①若AC为斜边，则1=x2+（3-x）2，即x2-3x+4=0，无解；②若AB为斜边，则x2=(3﹣x)2+1，解得x，满足1<x<2；③若BC为斜边，则(3﹣x)2=1+x2，解得：x，满足1＜x＜2；

解：

（1）∵MN=4，MA=1，AB=x，

∴BN=4﹣1﹣x=3﹣x，

由旋转的性质得：MA=AC=1，BN=BC=3﹣x，

由三角形的三边关系得

，

∴x的取值范围是1＜x＜2．

故答案为：1＜x＜2；

（2）∵△ABC是直角三角形，

∴若AC为斜边，则1=x2+(3﹣x)2，即x2﹣3x+4=0，无解，

若AB为斜边，则x2=(3﹣x)2+1，解得：x，满足1＜x＜2，

若BC为斜边，则(3﹣x)2=1+x2，解得：x，满足1＜x＜2，

故x的值为：x或x．

故答案为：x或x．