题目内容
【题目】如图,AB=AC,DB=DC,
(1)求证:AD平分∠BAC;
(2)延长CD与AB的延长线交于E ,延长AD到F,使DF=DC,连接EF,若∠C=100°,∠BAC=40°,求证:△EBD≌△EFD.

【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)易证△ABD≌△ACD,由此可得∠1=∠2,即AD平分∠BAC;
(2)由△ABD≌△ACD得∠1=∠2,∠ADB=∠ADC,即可证明△BDE≌△FDE.
试题解析:(1)证明:在△ABD和△ACD中,
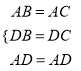 ,
,
∴ △ABD≌△ACD,
∴ ∠1=∠2,
∴ AD平分∠BAC;
(2)由(1)知 △ABD≌△ACD,
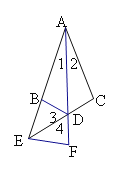
∴ ∠ADB=∠ADC,∠1=∠2,
在△ACE中,∠C=100°,∠BAC=40°,
∴∠1=∠2 =20°,
∴ ∠ADB=∠ADC=180°- ∠2 -∠C = 60°,
∴∠3=180°- ∠ADB-∠ADC=60°,
∵∠4=∠ADC=60°,
又DF=DC,DB=DC,
∴DB=DF,
在△BED和△EFD中,
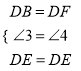 ,
,
∴△BED≌△EFD(SAS).

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目