题目内容
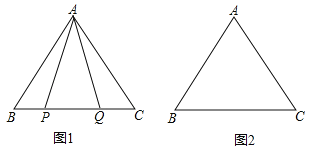
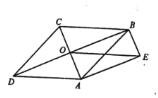
【题目】如图,平行四边形ABCD的对角线AC, BD相交于点O,且AE∥BD, BE∥AC, OE= CD.
(1)求证:四边形ABCD是菱形;
(2)若AD=2,则当四边形ABCD的形状是__________时,四边形AOBE的面积取得最大值是__________.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据平行四边形的性质和菱形的判定证明即可;
(2)根据正方形的判定和性质解答即可.
(1)∵AE∥BD,BE∥AC,
∴四边形AEBO是平行四边形,
∵四边形ABCD是平行四边形,
∴DC=AB.
∵OE=CD,
∴OE=AB,
∴平行四边形AEBO是矩形,
∴∠BOA=90°,
∴AC⊥BD,
∴平行四边形ABCD是菱形;
(2)正方形,面积为2;理由如下:
过点B作OE的垂线段BF交OE于点F
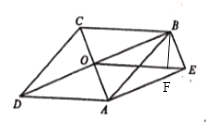
因为OE=CD=AD=2,
所以矩形AOBE的面积为2x![]() 0E:BF=2BF
0E:BF=2BF
当AB与OE垂直时,BF长达到最大值,
即AB长的一半,此时矩形的面积为2
当AB与0E垂直时平行四边形ABCD是正方形..

练习册系列答案
相关题目