题目内容
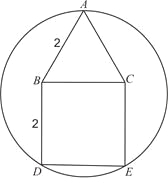
【题目】已知多边形ABDEC是由边长为2的等边三角形ABC和正方形BDEC组成,一圆过A、D、E三点,求该圆半径的长.
【答案】2
【解析】
作AF⊥BC,垂足为F,并延长交DE于H点.根据其轴对称性,则圆心必定在AH上.设其圆心是O,连接OD,OE.根据等边三角形的性质和正方形的性质,可以求得AH,DH的长,设圆的半径是r.在直角三角形BOH中,根据勾股定理列方程求解.
如图,
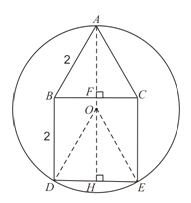
作AF⊥BC,垂足为F,并延长交DE于H点.
∵△ABC为等边三角形,
∴AF垂直平分BC,
∵四边形BDEC为正方形,
∴AH垂直平分正方形的边DE.
又DE是圆的弦,∴AH必过圆心,记圆心为O点,并设⊙O的半径为r.
在Rt△ABF中, ∵∠BAF=![]() ,
,
∴![]() .
.
∴OH=![]() =
=![]()
![]() r.
r.
在Rt△ODH中,![]() .
.
∴![]() .解得r=2.
.解得r=2.
∴该圆的半径长为2.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目