题目内容
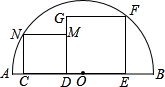如图，AB是半径为R的圆O的直径，四边形CDMN和DEFG都是正方形．其中C，D，E在AB上，F，N在半圆上．求证：两个正方形的面积之和为一定值．
分析：分别设出两个正方形的边长，连接ON，OF，在直角三角形中运用勾股定理表示CO，OE的长，把这两边的长与正方形的边长联系，得到等量关系，然后把得到的定理关系通过两边平方化简，求出两个正方形的面积的和．
解答：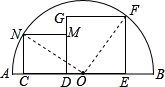
证明：如图，连接ON，OF，设正方形CDMN的边长为a，正方形DEFG的边长为b，
则OE=
，OC=
，而OD=OC-CD=DE-OE
∴有：
-a=b-
得到：
+
=a+b
两边平方得：R2-a2+2
•
+R2-b2=a2+2ab+b2
整理得：
•
=a2+b2+ab-R2
两边再次平方得：R4-（a2+b2）R2+a2b2=（a2+b2+ab）2-2（a2+b2+ab）R2+R4，
整理得：a2+b2=R2．
所以两个正方形的面积之和为一定值，这个值就是R2．
证明：如图，连接ON，OF，设正方形CDMN的边长为a，正方形DEFG的边长为b，则OE=
| R2-b2 |
| R2- a2 |
∴有：
| R2-a2 |
| R2-b2 |
得到：
| R2- a2 |
| R2- b2 |
两边平方得：R2-a2+2
| R2-a2 |
| R2-b2 |
整理得：
| R2-a2 |
| R2-b2 |
两边再次平方得：R4-（a2+b2）R2+a2b2=（a2+b2+ab）2-2（a2+b2+ab）R2+R4，
整理得：a2+b2=R2．
所以两个正方形的面积之和为一定值，这个值就是R2．
点评：本题考查的是垂径定理，连接ON，OF，得到两个直角三角形，根据勾股定理用二次根式表示OE，OC的长，然后由正方形的边长找到等量关系，通过两次两边平方确定根号，得到两个正方形的面积和与半径R的关系，确定两个正方形的面积和是一定值．
练习册系列答案
相关题目
如图， |
| AB |
|
| BC |
A、s=
| ||||
B、s=
| ||||
C、s=
| ||||
D、s=
|
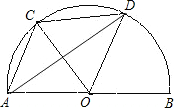
如图，
如图，AB是半径为10的⊙O的弦，OC⊥AB，垂足为点D，交⊙O于点C，且CD=2．求弦AB的长．
如图，AB是半径为R的圆O的直径，四边形CDMN和DEFG都是正方形．其中C，D，E在AB上，F，N在半圆上．求证：两个正方形的面积之和为一定值．