题目内容
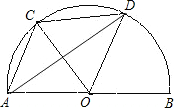 如图,
如图, |
| AB |
 |
| BC |
分析:过点D作DE⊥AB于E,则三角形AOD的面积s=
OA•DE.由于OA=1是定长,那么三角形AOD的面积s随DE的变化而变化,当DE取最小值时,s有最小值;当DE取最大值时,s有最大值.
| 1 |
| 2 |
解答: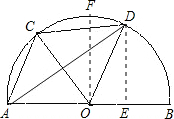 解:过点D作DE⊥AB于E,则三角形AOD的面积s=
解:过点D作DE⊥AB于E,则三角形AOD的面积s=
OA•DE.
∵OA=1,∴s=
DE.
过点O作OF⊥AB交⊙O于F,当点D与点F重合时,DE有最大值时,s也有最大值.此时OF=1,∴s=
;
当点D与点B重合时,DE有最小值0,s也有最小值0.
故0≤s≤
.
 解:过点D作DE⊥AB于E,则三角形AOD的面积s=
解:过点D作DE⊥AB于E,则三角形AOD的面积s=| 1 |
| 2 |
∵OA=1,∴s=
| 1 |
| 2 |
过点O作OF⊥AB交⊙O于F,当点D与点F重合时,DE有最大值时,s也有最大值.此时OF=1,∴s=
| 1 |
| 2 |
当点D与点B重合时,DE有最小值0,s也有最小值0.
故0≤s≤
| 1 |
| 2 |
点评:本题主要考查了三角形的面积.由于D是
上的一动点,能够结合三角形的面积公式,分析出D与半圆的中点F重合时,三角形AOD的面积s取最大值是解决本题的关键.
 |
| BC |

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 如图,
如图, |
| AB |
 |
| BC |
A、s=
| ||||
B、s=
| ||||
C、s=
| ||||
D、s=
|
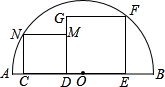 如图,AB是半径为R的圆O的直径,四边形CDMN和DEFG都是正方形.其中C,D,E在AB上,F,N在半圆上.求证:两个正方形的面积之和为一定值.
如图,AB是半径为R的圆O的直径,四边形CDMN和DEFG都是正方形.其中C,D,E在AB上,F,N在半圆上.求证:两个正方形的面积之和为一定值. 如图,AB是半径为10的⊙O的弦,OC⊥AB,垂足为点D,交⊙O于点C,且CD=2.求弦AB的长.
如图,AB是半径为10的⊙O的弦,OC⊥AB,垂足为点D,交⊙O于点C,且CD=2.求弦AB的长. 如图,AB是半径为R的圆O的直径,四边形CDMN和DEFG都是正方形.其中C,D,E在AB上,F,N在半圆上.求证:两个正方形的面积之和为一定值.
如图,AB是半径为R的圆O的直径,四边形CDMN和DEFG都是正方形.其中C,D,E在AB上,F,N在半圆上.求证:两个正方形的面积之和为一定值.