题目内容
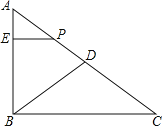
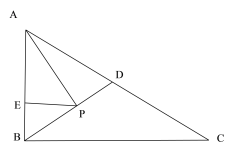
【题目】如图,在Rt△ABC中,∠ABC=90°,AC=15cm,BC=12cm,点D是线段AC的中点,动点P从A﹣D﹣B﹣C向终点C出发,速度为5cm/s,当点P不与点A、B重合时,作PE⊥AB交线段AB于点E,设点P的运动时间为t(s),△APE的面积为S(cm2).
(1)写出线段AB的长;
(2)当点P在线段BD上时,求PE的长(用含t的式子表示);
(3)当点P沿A﹣D﹣B运动时,用含t的代数式表示S;
(4)点E关于直线AP的对称点为E′,当点E′落在△ABC的内部时,直接写出t的取值范围.
【答案】(1)9;(2)12﹣4t;(3)S=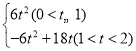 ;(4)
;(4)![]() <t<3或3<t<3.9
<t<3或3<t<3.9
【解析】
(1)在Rt△ABC中,根据勾股定理即可解决问题.
(2)只要证明△PBE∽△CAB,可得![]() ,由此即可解决问题.
,由此即可解决问题.
(3)分两种情形讨论①当0<t≤3时.②当3<t<6时,根据三角形的面积公式求出AE、PE即可解决问题.
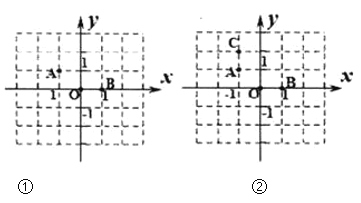
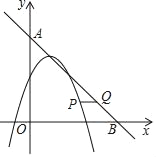
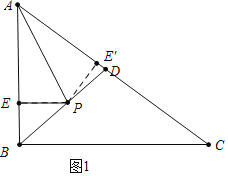
(4)求出两个特殊点的时间①如图1中,当点E关于AP的对称点E′在线段AC上时.如图2中,当点P在BC上,点E关于AP的对称点E′在线段AC上时.即可解决问题.
(1)∵在Rt△ABC中,∠ABC=90°,AC=15cm,BC=12cm,
∴AB=![]() ,
,
即AB的长为9;
(2)∵PE⊥AB,BC⊥AB,
∴PE∥BC,∠ABC=∠BEP=90°,
∴∠EPB=∠PBC,
∵点D为AC中点,
∴BD=CD=![]() AC,
AC,
∴∠DBC=∠DCB,
∴∠EPB=∠DCB,
∴△PBE∽△CAB,
∴![]()
∴![]() ,
,
∵BP=15﹣5t,
∴PE=12﹣4t.
(3)当0<t≤3时
AE=5t×![]() =3t,PE=5t×
=3t,PE=5t×![]() =4t,
=4t,
S=![]() PEAE=
PEAE=![]() 4t3t=6t2,
4t3t=6t2,
∴S=6t2.
当3<t<6时,
AE=9﹣(15﹣5t)×![]() =3t,PE=(15﹣5t)×
=3t,PE=(15﹣5t)×![]() =12﹣4t,
=12﹣4t,
S=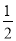 PEAE=
PEAE=![]() 3t(12﹣4t)=﹣6t2+18t.
3t(12﹣4t)=﹣6t2+18t.
∴S=﹣6t2+18t,
综上所述,S=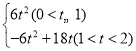 .
.
(4)如图1中,当点E关于AP的对称点E′在线段AC上时.作PE′⊥AC于E′,则PE=PE′
∵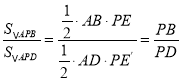 ,
,
∴![]() ,
,
∴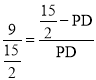 ,
,
∴PD=![]() ,
,
∴点P运动的时间=(![]() )÷5=
)÷5=![]() s,
s,
观察图象可知当![]() <t<3时,当点E′落在△ABC的内部.
<t<3时,当点E′落在△ABC的内部.
如图2中,当点P在BC上,点E关于AP的对称点E′在线段AC上时.
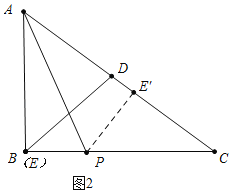
同理可得![]() ,
,
∴![]() ,
,
∴PB=4.5,
∴∴点P运动的时间=(![]() +4.5)÷5=3.9s
+4.5)÷5=3.9s
观察图象可知当3<t<3.9时,当点E′落在△ABC的内部.
综上所述,当![]() <t<3或3<t<3.9时,当点E′落在△ABC的内部.
<t<3或3<t<3.9时,当点E′落在△ABC的内部.

【题目】我市某中学开展“社会主义核心价值观”演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.根据图中数据解决下列问题:

(1)根据图示求出表中的![]() 、
、![]() 、
、![]()
平均数 | 中位数 | 众数 | |
九(1) |
| 85 |
|
九(2) | 85 |
| 100 |
![]() ,
,![]() ,
,![]() .
.
(2)小明同学已经算出了九(2)班复赛成绩的方差:
![]() ,请你求出九(1)班复赛成绩的方差
,请你求出九(1)班复赛成绩的方差![]() ;
;
(3)根据(1)、(2)中计算结果,分析哪个班级的复赛成绩较好?