题目内容
阅读材料:例:说明代数式
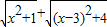 的几何意义,并求它的最小值.
的几何意义,并求它的最小值.解:
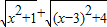 =
=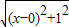 +
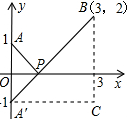
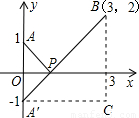
+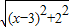 ,如图,建立平面直角坐标系,点P(x,0)是x轴上一点,则
,如图,建立平面直角坐标系,点P(x,0)是x轴上一点,则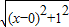 可以看成点P与点A(0,1)的距离,
可以看成点P与点A(0,1)的距离,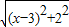 可以看成点P与点B(3,2)的距离,所以原代数式的值可以看成线段PA与PB长度之和,它的最小值就是PA+PB的最小值.
可以看成点P与点B(3,2)的距离,所以原代数式的值可以看成线段PA与PB长度之和,它的最小值就是PA+PB的最小值.设点A关于x轴的对称点为A′,则PA=PA′,因此,求PA+PB的最小值,只需求PA′+PB的最小值,而点A′、B间的直线段距离最短,所以PA′+PB的最小值为线段A′B的长度.为此,构造直角三角形A′CB,因为A′C=3,CB=3,所以A′B=3
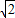 ,即原式的最小值为3
,即原式的最小值为3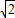 .
.根据以上阅读材料,解答下列问题:
(1)代数式
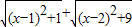 的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B______的距离之和.(填写点B的坐标)
的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B______的距离之和.(填写点B的坐标)(2)代数式
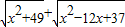 的最小值为______.
的最小值为______.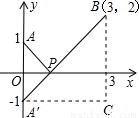
【答案】分析:(1)先把原式化为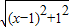 +
+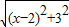 的形式,再根据题中所给的例子即可得出结论;
的形式,再根据题中所给的例子即可得出结论;
(2)先把原式化为 +
+ 的形式,故得出所求代数式的值可以看成平面直角坐标系中点P(x,0)与点A(0,7)、点B(6,1)的距离之和,再根据在坐标系内描出各点,利用勾股定理得出结论即可.
的形式,故得出所求代数式的值可以看成平面直角坐标系中点P(x,0)与点A(0,7)、点B(6,1)的距离之和,再根据在坐标系内描出各点,利用勾股定理得出结论即可.
解答: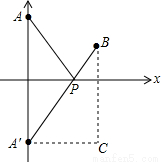 解:(1)∵原式化为
解:(1)∵原式化为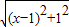 +
+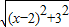 的形式,
的形式,
∴代数式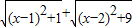 的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B(2,3)的距离之和,
的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B(2,3)的距离之和,
故答案为(2,3);
(2)∵原式化为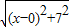 +
+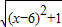 的形式,
的形式,
∴所求代数式的值可以看成平面直角坐标系中点P(x,0)与点A(0,7)、点B(6,1)的距离之和,
如图所示:设点A关于x轴的对称点为A′,则PA=PA′,
∴PA+PB的最小值,只需求PA′+PB的最小值,而点A′、B间的直线段距离最短,
∴PA′+PB的最小值为线段A′B的长度,
∵A(0,7),B(6,1)
∴A′(0,-7),A′C=6,BC=8,
∴A′B=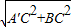 =
=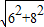 =10,
=10,
故答案为:10.
点评:本题考查的是轴对称-最短路线问题,解答此题的关键是根据题中所给给的材料画出图形,再利用数形结合求解.
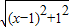 +
+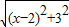 的形式,再根据题中所给的例子即可得出结论;
的形式,再根据题中所给的例子即可得出结论;(2)先把原式化为
 +
+ 的形式,故得出所求代数式的值可以看成平面直角坐标系中点P(x,0)与点A(0,7)、点B(6,1)的距离之和,再根据在坐标系内描出各点,利用勾股定理得出结论即可.
的形式,故得出所求代数式的值可以看成平面直角坐标系中点P(x,0)与点A(0,7)、点B(6,1)的距离之和,再根据在坐标系内描出各点,利用勾股定理得出结论即可.解答:
 解:(1)∵原式化为
解:(1)∵原式化为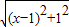 +
+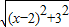 的形式,
的形式,∴代数式
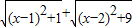 的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B(2,3)的距离之和,
的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B(2,3)的距离之和,故答案为(2,3);
(2)∵原式化为
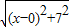 +
+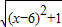 的形式,
的形式,∴所求代数式的值可以看成平面直角坐标系中点P(x,0)与点A(0,7)、点B(6,1)的距离之和,
如图所示:设点A关于x轴的对称点为A′,则PA=PA′,
∴PA+PB的最小值,只需求PA′+PB的最小值,而点A′、B间的直线段距离最短,
∴PA′+PB的最小值为线段A′B的长度,
∵A(0,7),B(6,1)
∴A′(0,-7),A′C=6,BC=8,
∴A′B=
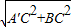 =
=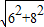 =10,
=10,故答案为:10.
点评:本题考查的是轴对称-最短路线问题,解答此题的关键是根据题中所给给的材料画出图形,再利用数形结合求解.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
 (2012•十堰)阅读材料:
(2012•十堰)阅读材料: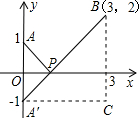
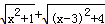 的几何意义,并求它的最小值.
的几何意义,并求它的最小值.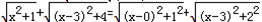 ,如图,建立平面直角坐标系,点P (x ,0 )是x 轴上一点,则
,如图,建立平面直角坐标系,点P (x ,0 )是x 轴上一点,则 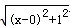 可以看成点P 与点A (0 ,1 )的距离,
可以看成点P 与点A (0 ,1 )的距离, 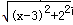 可以看成点P 与点B (3 ,2 )的距离,所以原代数式的值可以看成线段PA 与PB 长度之和,它的最小值就是PA+PB 的最小值.
可以看成点P 与点B (3 ,2 )的距离,所以原代数式的值可以看成线段PA 与PB 长度之和,它的最小值就是PA+PB 的最小值.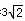
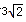
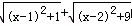 的值可以看成平面直角坐标系中点P (x ,0 )与点A(1 ,1)、点B ( )的距离之和.(填写点B 的坐标)
的值可以看成平面直角坐标系中点P (x ,0 )与点A(1 ,1)、点B ( )的距离之和.(填写点B 的坐标)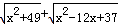 的最小值为( ).
的最小值为( ).