��Ŀ����
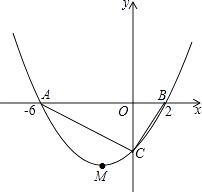
����Ŀ����ͼ1��ֱ��y=�� ![]() x+8����x�ᡢy��ֱ��ڵ�A��C����ACΪ�Խ���������OABC����P��Q�ֱ�Ϊ����OC������AC�ϵĶ��㣬����AQ=2CP������PQ�����P������ΪP��0��t����
x+8����x�ᡢy��ֱ��ڵ�A��C����ACΪ�Խ���������OABC����P��Q�ֱ�Ϊ����OC������AC�ϵĶ��㣬����AQ=2CP������PQ�����P������ΪP��0��t����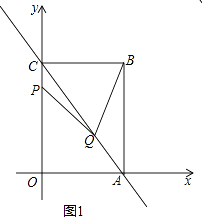
��1�����B�����꣮
��2����t=1ʱ������BQ�����ABQ�������
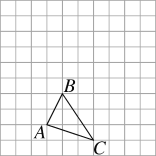
��3����ͼ2����PQΪֱ������I���ǡ�I������AC����һ������ΪE��
���� ![]() =
= ![]() �����ʱt��ֵ��
�����ʱt��ֵ��
����Բ��I�ڡ�ABC�ڲ������������ϣ������ʱt��ȡֵ��ΧΪ�Ƕ���?
���𰸡�
��1���⣺��x=0����y=�� ![]() x+8����y=8����C��0��8����
x+8����y=8����C��0��8����
��y=0����y=�� ![]() x+8����x=6����A��6��0����
x+8����x=6����A��6��0����
���ı���OABC�Ǿ��Σ���B��6��8��
��2���⣺��ͼ1��

��QH��AB��H����t=1ʱ��CP=7��AQ=14��
��֤AC=10��sin��BAC= ![]() ��
��
��QH=AQsin��BAC= ![]() ��
��
��S��ABQ= ![]() ��
��
��3���⣺���ࣺ����ͼ2��

��P���߶�OC�ϣ�Q���߶�AC��ʱ����3����8ʱ��
��֤ ![]() =sin��EQP=sin��ACO=
=sin��EQP=sin��ACO= ![]() �����EQP=��ACO����CP=PQ��
�����EQP=��ACO����CP=PQ��
��PE��CQ����CE=EQ����2�� ![]() ��8��t��=10����16��2t�������t1=
��8��t��=10����16��2t�������t1= ![]() ��
��
��Q��C�غϣ�P��OC��ʱ����ͼ3��

�ɵ�16��2t=10�����t2=3��
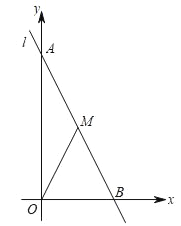
��Q��C�غϣ�P��OC�ӳ�����ʱ����ͼ4��

�ɵ�2t��16=10�����t3=13��
������P��OC�ӳ����ϣ�Q��AC�ӳ�����ʱ����ͼ5��

ͬ�ɵá�Q=��PCQ��
��CP=PQ���� ![]() ��2t��16��10��=
��2t��16��10��= ![]() ��t��8�������t4=33��
��t��8�������t4=33��
��t= ![]() ��3��13��33��
��3��13��33��
�ڵ�Բ��I�ڱ�AC��ʱ����ͼ6��P��C�غϣ�Q��A�غϣ�
��OP=t=8��

��Բ��I�ڱ�BC��ʱ�����I��x�ύ��F������FQ��
��PQ��ֱ����
��QF��x�ᣬ
��FQ��OA��CP=CF=t��8��
���CQF�ס�ACO��
�� ![]() =
= ![]() ����
���� ![]() =
= ![]() ��
��
��t= ![]() ��
��

����Բ��I�ڡ�ABC�ڲ������������ϣ������ʱt��ȡֵ��ΧΪ8��t�� ![]() ��
��
�ʴ�Ϊ��8��t�� ![]()
����������1����x=0����y=�� ![]() x+8����y=8����y=0����y=��
x+8����y=8����y=0����y=�� ![]() x+8����x=6�����ǵõ����ۣ���2����ͼ1����QH��AB��H����t=1ʱ��CP=7��AQ=14����ֱ�������εõ�QH=AQsin��BAC=
x+8����x=6�����ǵõ����ۣ���2����ͼ1����QH��AB��H����t=1ʱ��CP=7��AQ=14����ֱ�������εõ�QH=AQsin��BAC= ![]() �����������ε������ʽ���ɵõ����ۣ���3������ͼ2����P���߶�OC�ϣ�Q���߶�AC��ʱ����ֱ�������εõ����t1=
�����������ε������ʽ���ɵõ����ۣ���3������ͼ2����P���߶�OC�ϣ�Q���߶�AC��ʱ����ֱ�������εõ����t1= ![]() ����Q��C�غϣ�P��OC��ʱ����ͼ3�����t2=3����Q��C�غϣ�P��OC�ӳ�����ʱ����ͼ4�����t3=13��������P��OC�ӳ����ϣ�Q��AC�ӳ�����ʱ����ͼ5��ͬ���t4=33���ڵ�Բ��I�ڱ�AC��ʱ����ͼ6��P��C�غϣ�Q��A�غϣ����OP=t=8����Բ��I�ڱ�BC��ʱ�����I��x�ύ��F������FQ���������������ε����ʵõ�t=
����Q��C�غϣ�P��OC��ʱ����ͼ3�����t2=3����Q��C�غϣ�P��OC�ӳ�����ʱ����ͼ4�����t3=13��������P��OC�ӳ����ϣ�Q��AC�ӳ�����ʱ����ͼ5��ͬ���t4=33���ڵ�Բ��I�ڱ�AC��ʱ����ͼ6��P��C�غϣ�Q��A�غϣ����OP=t=8����Բ��I�ڱ�BC��ʱ�����I��x�ύ��F������FQ���������������ε����ʵõ�t= ![]() �����ǵõ����ۣ�
�����ǵõ����ۣ�
�����㾫����������Ҫ���������������ε�Ӧ�õ����֪ʶ�㣬��Ҫ���ղ�ߣ��������ܵ��ﶥ��������ĸ߶ȣ�ͨ���á���ͬһʱ�������Ӱ���ɱ�������ԭ���������ࣺ�������ܵ��������ľ�����������������������������ȷ�����⣮

����Ŀ��Ϊ�˼�ǿ����Ľ�ˮ��ʶ����������ˮ��Դ��ij�в��ü۸�����ֶδﵽ��ˮ��Ŀ�ģ���������ˮ�շѼ۸����Ŀ����
��Ŀ��
ÿ��ˮ���� | ���� |
������ |
|
���� |
|
���� |
|
ע��ˮ�Ѱ��½���.
��ij������![]() �·���ˮ
�·���ˮ![]() ����Ӧ��ˮ�ѣ�
����Ӧ��ˮ�ѣ�![]() Ԫ��
Ԫ��
��1�����û�����![]() �·���ˮ
�·���ˮ![]() ����Ӧ��ˮ��_______Ԫ��
����Ӧ��ˮ��_______Ԫ��
��2�����û�����![]() ��
��![]() �·ݹ���ˮ
�·ݹ���ˮ![]() ��
��![]() �·���ˮ������
�·���ˮ������![]() �·ݣ�������ˮ��
�·ݣ�������ˮ��![]() Ԫ����û�����
Ԫ����û�����![]() �·ݸ���ˮ���������ף�
�·ݸ���ˮ���������ף�