题目内容
【题目】已知:点D是△ABC所在平面内一点,连接AD、CD.
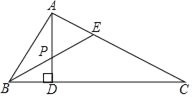
(1)如图1,若∠A=28°,∠B=72°,∠C=11°,求∠ADC;
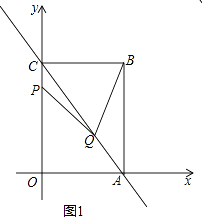
(2)如图2,若存在一点P,使得PB平分∠ABC,同时PD平分∠ADC,探究∠A,∠P,∠C的关系并证明;
(3)如图3,在 (2)的条件下,将点D移至∠ABC的外部,其它条件不变,探究∠A,∠P,∠C的关系并证明.

【答案】(1) 111 ;(2) ∠A-∠C=2∠P,理由见解析;(3) ∠A+∠C=2∠P,理由见解析.
【解析】
(1)延长AD交BC于E,利用三角形外角的性质即可求解;
(2)∠A-∠C=2∠P,由三角形外角等于不相邻的两个内角的和以及(1)结论即可求解;
(3)∠A+∠C=2∠P,由(2)结论以及角平分线的性质即可得到.
(1)如图1,延长AD交BC于E,

在△ABE中,∠AEC=∠A+∠B=28+72=100,
在△DEC中,∠ADC=∠AEC+∠C=100+11=111 ;
(2)∠A-∠C=2∠P,理由如下:
如图2,

∠5=∠A+∠1,∠5=∠P+∠3
∴∠A+∠1=∠P+∠3
∵PB平分∠ABC,PD平分∠ADC
∴ ∠1=∠2,∠3=∠4
∴∠A+∠2=∠P+∠4
由(1)知∠4=∠2+∠P+∠C
∴∠A+∠2=∠P+∠2+∠P+∠C
∴∠A-∠C=2∠P
(3)∠A+∠C=2∠P,理由如下:
如图3,
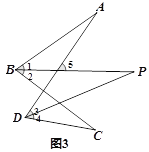
同(2)理知∠A+∠1=∠P+∠3,∠C+∠4=∠P+∠2
∴∠A+∠C+∠1+∠4=2∠P+∠2+∠3
∵PB平分∠ABC,PD平分∠ADC
∴ ∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
∴∠A+∠C=2∠P

练习册系列答案
相关题目