题目内容
【题目】在平面直角坐标系xOy中,点P的坐标为![]() ,点Q的坐标为
,点Q的坐标为![]() ,且
,且![]() ,
,![]() ,若P,Q为某正方形的两个顶点,且该正方形的边均与某条坐标轴平行(含重合),则称P,Q互为“正方形点”(即点P是点Q的“正方形点”,点Q也是点P的“正方形点”).下图是点P,Q互为“正方形点”的示意图.
,若P,Q为某正方形的两个顶点,且该正方形的边均与某条坐标轴平行(含重合),则称P,Q互为“正方形点”(即点P是点Q的“正方形点”,点Q也是点P的“正方形点”).下图是点P,Q互为“正方形点”的示意图.

已知点A的坐标是(2,3),下列坐标中,与点A互为“正方形点”的坐标是____________.(填序号)
①(1,2);②(-1,5);③(3,2).
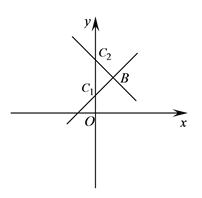
(2)若点B(1,2)的“正方形点”C在y轴上,求直线BC的表达式;
(3)点D的坐标为(-1,0),点M的坐标为(2,m),点N是线段OD上一动点(含端点),若点M,N互为“正方形点”,求m的取值范围.
【答案】(1) ①③;(2) ![]() 或
或 ![]() ;(3)
;(3) ![]() 或
或![]() .
.
【解析】(1)根据点A互为“正方形点”的坐标定义即可求出所求的坐标;(2)由已知条件先求出点C的坐标,利用待定系数法求得直线BC的表达式;(3)由点N是线段OD上一动点(含端点),求出点D、O的正方形点坐标,结合图象写出m的取值范围.
解:(1)①③
(2)∵点B(1,2)的“正方形点”C在y轴上,
∴点C的坐标为(0,1),(0,3),
∴直线BC的表达式为![]() ,
,![]() .
.
(3)过点OD分别作与x轴夹角为![]() 的直线,
的直线,
∵点M的坐标为(2,m),点N是线段OD上一动点(含端点),
点M,N互为“正方形点”,
∴点D的正方形点坐标是(2,3),(2,-3),
点O的正方形点坐标是(2,2),(2,-2),
∴![]() 或
或![]() .
.

“点睛”本题考查了新定义问题,涉及到一次函数的知识,解题时要理解“正方形点”的定义,对学生的综合能力要求即较高,一定要注意将新知识贯穿整个解题中.

练习册系列答案
相关题目

