题目内容
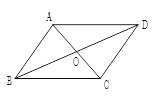
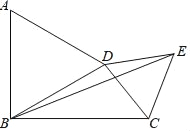
【题目】如图,△ABD、△CDE是两个等边三角形,连接BC、BE.若∠DBC=30°,BD=2,BC=3,则BE=_____.
【答案】![]()
【解析】
连接AC,根据题意易证△ACD≌△BED(SAS),根据全等三角形的性质可得AC=BE,再根据勾股定理求出AC的值即可得出结论.
连接AC,
∵△ABD、△CDE是两个等边三角形,
∴AB=BD=AD=2,CD=DE,∠ABD=∠ADB=∠CDE=60°,
∴∠ADB+∠BDC=∠CDE+∠BDC,
∴∠ADC=∠BDE,
在△ACD与△BED中
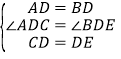 ,
,
∴△ACD≌△BED(SAS),
∴AC=BE,
∵∠DBC=30°,
∴∠ABC=∠ABD+∠DBC=60°+30°=90°,
在Rt△ABC中,AB=2,BC=3,
∴AC=![]() =
=![]() =
=![]() ,
,
∴BE=![]() .
.
故答案为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目