题目内容
【题目】如图，在边长为1个单位长度的小正方形网格中.
(1)画出△ABC关于直线x=l对称的△A1BlC1.
(2)画出△ABC关于C点顺时针旋转90o的△A2B2C2.
(3)设P、Q两点分别是△ABC和△A1BlC1两对应点,已知P点坐标为(m,n),写出点Q的坐标.
【答案】（1）图略；（2）图略；（3）Q（2-m，n）
【解析】试题分析：（1）分别作出点A、C关于x=1的对称点，顺次连接即可得；
（2）分别作出点A、B关于C点顺时针旋转90°所得对应点，再顺次连接即可得；
（3）根据轴对称的性质求解可得．
试题解析：解：（1）如图，△A1B1C1即为所求；
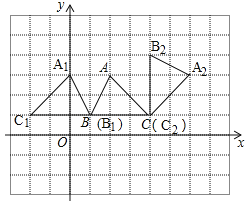
（2）如图，△A2B2C2即为所求；
（3）∵P、Q两点分别是△ABC和△A1B1C1两对应点，且△ABC与△A1B1C1关于直线x=1的对称，∴P、Q两点的纵坐标相等，点Q的横坐标满足
=1，即x=2﹣m，∴点Q的坐标为（2﹣m，n）．
练习册系列答案
相关题目
【题目】下表是某校九年级(1)班20名学生某次数学测验的成绩统计表：
成绩(分) | 60 | 70 | 80 | 90 | 100 |
人数(人) | 1 | 5 | x | y | 2 |
(1)若这20名学生成绩的平均分数为82分，求x和y的值；
(2)在(1)的条件下，设这20名学生本次测验成绩的众数为a，中位数为b，求a，b的值．
